SICP 연습문제 1.14 친절한 풀이

문제

11센트를 동전으로 바꿀 때, 1.2.2절의 count-change 프로시저가 만들어 내는 프로세스를 나무꼴로 그려 보아라. 바꿀 돈이 늘어남에 따라 프로세스가 거치는 단계 수와 기억공간의 크기는 어떤 자람차수를 보이는가? (즉 어느정도로 자라나는가?)

문제로 부터 얻은 것

되도는 프로세스의 공간복잡도를 계산할 때, 사용하는 메모리의 크기는 가장 긴 가지의 길이라는 것을 이해했습니다.
어떤 프로세스의 부분 프로세스의 시간복잡도를 계산함으로써 그 프로세스의 시간복잡도를 계산할 수 있다는 것을 이해했습니다.

문제풀이

문제에서 직접 언급하지는 않았지만, (cc n 5)의 자람차수를 구하라는 말과 동일하다고 생각했습니다.
문제를 쉽게 이해하기 위해 프로세스가 자라나는 모양을 다이어그램으로 그려보았습니다.

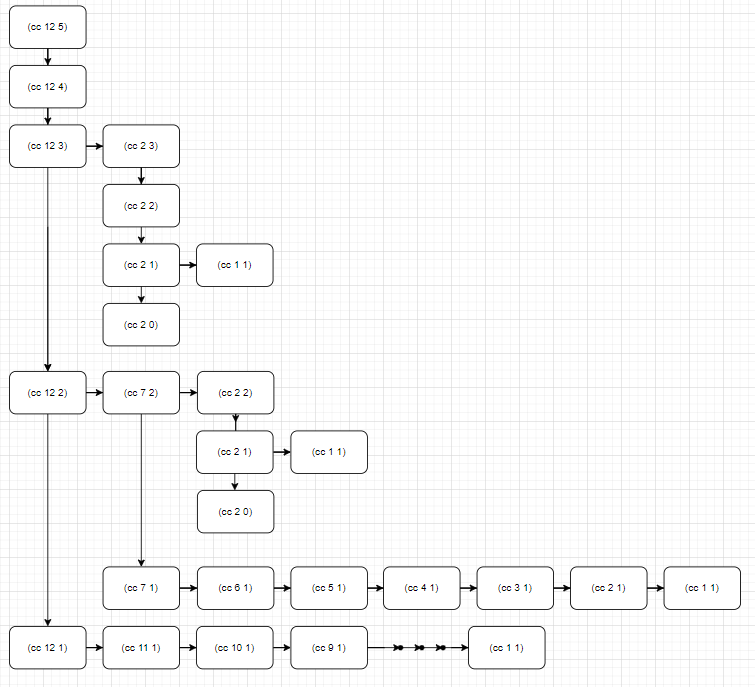
1. 공간복잡도

공간복잡도는 프로세스가 자라나면서 차지하는 메모리의 크기를 뜻합니다.
처음 이 문제를 풀 때에는 이렇게 생각했습니다.
“어? 맞바꿈 계산법으로 바꾸면 작은 프로세스 하나 하나마다 메모리 공간을 차지할 것이고, 결국 시간복잡도와 공간복잡도가 같지 않나?”
당연히 이 생각은 틀렸습니다.
위의 문제처럼 재귀호출방식으로 프로세스가 자라나는 경우에는 하나의 가지를 다 계산한 다음에 다시 돌아와서 다른 가지를 다 계산하는 방식을 사용합니다.
좀 더 컴퓨터과학적으로 표현하자면, DFS를 하는 것입니다.
즉 하나의 가지를 메모리에 적재한 체로 계산중일때, 다른 가지들은 계산중에 있지 않다는 말입니다.
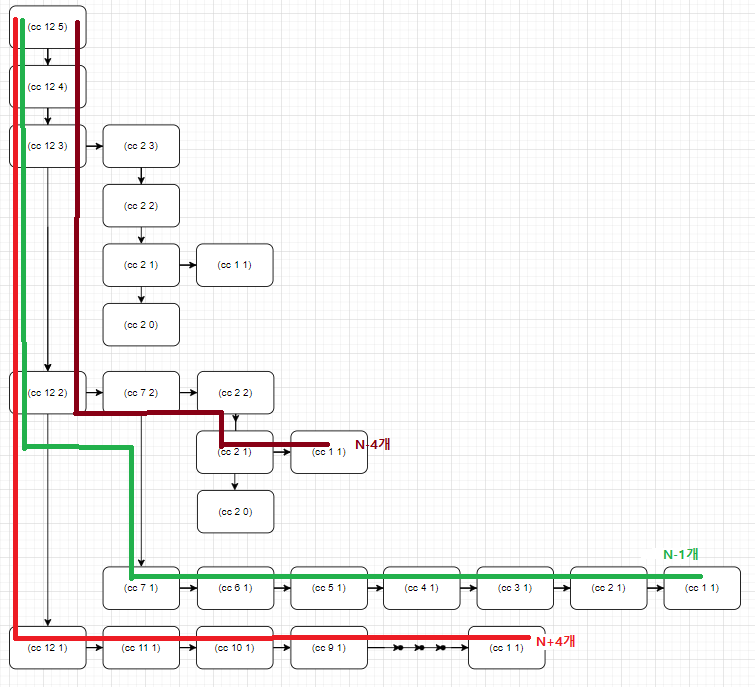
그렇게 되면 필요한 메모리의 크기는 결국 나무꼴의 프로세스 모양에서 가장 긴 가지의 길이만큼이 되는 것입니다.
위 프로세스에서 가장 긴 가지의 길이는 N+4입니다.

즉 프로시저의 공간복잡도는 $Θ(n)$입니다.

2. 시간복잡도

a. (cc n 1)

시간복잡도를 쉽게 계산하기 위해서는 (cc n 1)부터 알아볼 필요가 있습니다.
(cc n 1)의 시간복잡도가 $Θ(n)$인 것은 쉽게 알 수 있습니다.

(cc 12 1)
(cc 11 1)
(cc 10 1)
(cc 9 1)
(cc 8 1)
   :
(cc 1 1)

b. (cc n 2)

프로세스의 진행을 쉽게 보기 위해 다이어그램을 그려보았습니다.

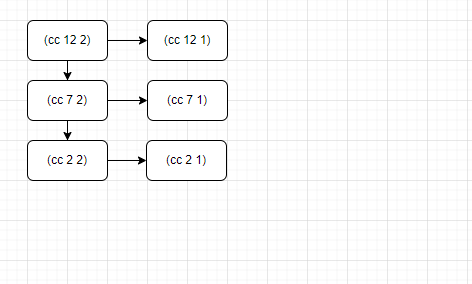
위 그림에서 알 수 있듯
(cc n 2)프로세스는 n이 5씩 커질때 마다 (cc n 1)프로세스를 하나씩 만들어 냅니다.
아시다시피 (cc n 1)프로세스의 시간복잡도는 n입니다.
그러므로 (cc n 2)의 시간복잡도는 (cc n 1)프로세스들의 계산단계들을 모두 더한 것이라고 볼 수 있습니다.
(cc n 1)프로세스들의 계산단계의 갯수는 n개 n-5개 n-10개… 라고 할 수 있습니다.

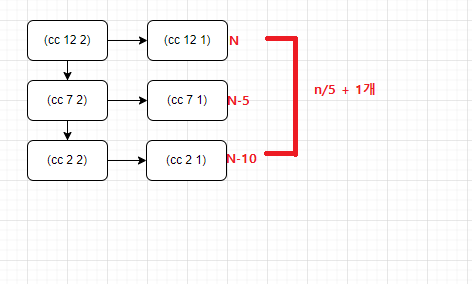
또 그 프로세스들의 개수는 $\frac{n}{5}+1$과 같습니다.
이것을 계산해 보면, 그 값은 $n\times(\frac{n}{5}+1)$보다 작고 $(n-k)\times(\frac{n}{5}+1)$보다 큼을 알 수 있습니다. (위의 예시에서 k는 10)
$∴$ (cc n 2)는 $Θ(n^2)$를 따른다.

c. (cc n 5)

위와 같은 방법으로
(cc n 3)는 $Θ(n^3)$
(cc n 4)는 $Θ(n^4)$
(cc n 5)는 $Θ(n^5)$
를 따른다는 것을 쉽게 알아낼 수 있습니다.

이 문제는 노트에 직접 풀어보시는 것을 추천드립니다.

읽어주셔서 감사합니다.