SICP 연습문제 1.17 & 1.18 친절한 풀이

문제

이 절에서 나오는 거듭제곱 알고리즘은 여러 번 곱셈을 거듭하여 값을 구한다는 단순한 생각에 뿌리를 둔다. 이와 비슷하게 곱셈도 덧셈을 거듭하는 것으로 나타낼 수 있다. 다음은 expt 프로시저처럼 (언어에서 덧셈만 있고 곱셈은 없다 치고) 덧셈으로 곱셈 프로시저를 짜본 것이다.

(define (* a b)
  (if (= b 0)
      0
      (+ a (* a (- b 1)))))

이 알고리즘의 계산 단계는 b와 나란히 (즉, 선형 비례로) 자란다. 이때 덧셈 말고도, 정수 값을 두배로 하거나 (짝수를) 반으로 나누는 프로시저 double과 halve가 이미 있었다고 치자. 이 프로시저를 써서, fast-expt처럼 계산단계가 로그비례로 자라나는 곱셈 프로시저를 짜보라.

문제로 부터 얻은 것

프로세스가 자라날때 반복수를 반으로 줄일 수 있는 방법이 있다면,
프로시저를 $Θ(\log{n})$으로 만들기 쉽다는 것을 알수 있었습니다.

문제풀이

문제 풀이의 기본 아이디어는 앞의 절을 잘 이해하였다면 가볍게 얻을 수 있을 것이라 생각합니다.
제가 떠올린 아이디어는 이렇습니다.

(mult-iter a b temp)프로시저를 만들어서,
$a \times b + temp$를 일정하게 유지하면서 b를 1로 만들자.

이 아이디어는 연습문제1.16의 아이디어와 결이 같습니다.
$a \times b + temp$를 어떻게 잘 변형하다가,
결국 마지막에 b가 1이 되었을때, (+ a temp)를 반환하면 문제가 해결되는 것입니다.

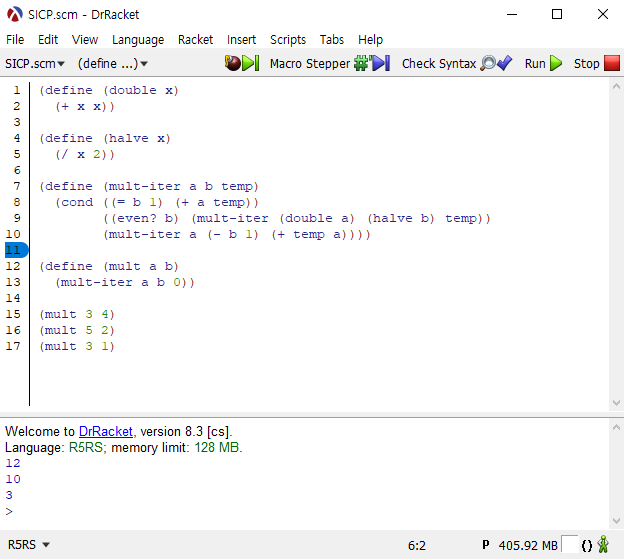
그렇게 어렵지 않게 구현할 수 있었습니다.
물론 이 프로시저는 약간의 문제가 있습니다.
b가 0이나 음수일 때는 의도에 맞게 동작하지 않습니다.
해결 방법이 그렇게 어려울 것 같지 않고, 문제의 풀이의도와는 동떨어진 내용이므로 생략하겠습니다.

읽어주셔서 감사합니다.