SICP 연습문제 1.22 친절한 풀이

문제

대개 Lisp 시스템에는 runtime이라는 기본 프로시저가 있어서, 이것으로 시스템이 실제 돌아간 시간을 (이를테면, 마이크로 초 단위로 잰) 정수 값으로 얻을 수 있다. (dr.racket은 아닙니다. 이 글을 참고해서 별도로 설정해줘야 runtime을 쓸 수 있습니다.) 아래 timed-prime-test는 정수 n을 받아서 찍은 다음 그 값이 소수인지 따져보는 프로시저로, n이 소수면 별표 세 개와 함께 검사하는 데 걸린 시간을 찍는다.

(define (report-prime elapsed-time)
  (display "***")
  (display elapsed-time))

(define (start-prime-test n start-time)
  (if (prime? n)
      (report-prime (- (runtime) start-time))))

(define (timed-prime-test n)
  (newline)
  (display n)
  (start-prime-test n (runtime)))

이 프로시저를 써서, 정해진 넓이에 속하는 홀수를 차례로 찾아 소수인지 알아볼 수 있도록 search-for-primes 프로시저를 짜라. 이 프로시저로 1,000과 100,000과 1,000,000보다 큰 소수 가운데 처음 나오는 3개를 찾아보아라. 또, 소수인지 따져 보는 데 시간이 얼마나 걸리는지 눈여겨보자. 검사하는 알고리즘의 자람차수가 $Θ(\sqrt{}{n})$이므로 10,000 언저리에 있는 소수를 찾을 때 드는 시간이 1,000 언저리에 있는 소수를 찾을 때보다 $\sqrt{}{10}$배 정도 많을 것이라 짐작할 수 있다. 실제 시간을 재어 보니 참말 그러한가? 100,000과 1,000,000 언저리를 뒤져보고 계산 시간을 쟀을 때에도 $\sqrt{}{n}$이라는 짐작을 뒷받침하는가? 프로그램을 돌리는 데 드는 시간이, 자라나는 계산 단계 수에 비례하여 늘어난다는 생각이 이 실험 결과와 잘 맞아떨어지는가?

문제로 부터 얻은 것

시간복잡도와 실제 성능의 오차를 확인할 수 있었습니다.

문제풀이

책에 실려있는 prime?프로시저는 다음과 같습니다.

(define (divides? a b)
  (= (remainder a b) 0))

(define (find-divisor n test-divisor)
  (cond ((> (square test-divisor) n) n)
        ((divides? n test-divisor) test-divisor)
        (else (find-divisor n (+ test-divisor 1)))))

(define (smallest-divisor n)
  (find-divisor n 2))

(define (prime? n)
  (= (smallest-divisor n) n))

저는 이 문제에서 준 코드를 다음과 같이 수정했습니다.

(define (report-prime elapsed-time n)
  (newline)
  (display n)
  (display "***")
  (display elapsed-time))

(define (start-prime-test n start-time)
  (if (prime? n)
      (report-prime (- (runtime) start-time) n)))

(define (timed-prime-test n)
  (start-prime-test n (runtime)))

문제에서 제공한 코드를 사용하게 되면, 소수가 아닌 수까지 화면에 표시되서 보기에 불편했습니다.
위의 코드로 수정하면 n이 소수일때만 표시됩니다.

search-for-primes프로시저는 아래와 같이 구현했습니다.

(define (iter from to)
  (cond ((> from to) (display "\nend"))
        (else (timed-prime-test from)
              (iter (+ 2 from) to))))

(define (search-for-primes from to)
  (if (even? from)
      (iter (+ from 1) to)
      (iter from to)))

아래 3줄의 코드를 실행해 보았습니다.

(search-for-primes 100000 100200)
(search-for-primes 10000000 10000200)
(search-for-primes 1000000000 1000000200)

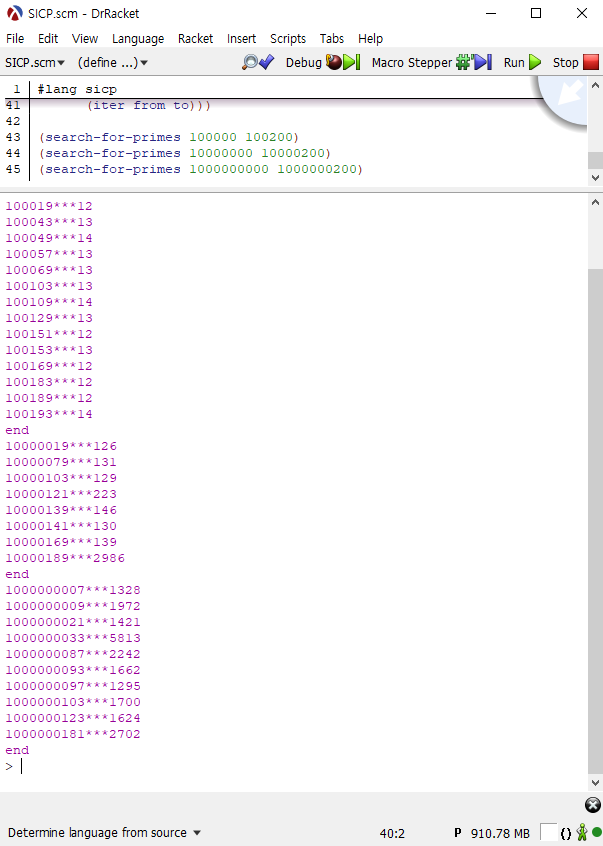
n이 100배씩 커진 만큼 자리수가 한자리씩 변하는 것을 볼 수 있습니다.
하지만 정확하게 10배는 아닌 것도 확인할 수 있습니다.
저는 두가지의 원인을 생각했습니다.
첫번째 이유는 $Θ(\sqrt{n})$이 최악의 경우와 최선의 경우를 생각하지 않은 러프한 추측이기 때문입니다.
두번째 이유는 if식이나 기타 다른 프로시저들이 차지하는 시간이 $Θ(\sqrt{n})$식에 포함되어 있지 않아 생긴 현상인 것 같습니다.
시간복잡도와 실제 러닝타임의 오차를 확인할 수 있었습니다.

읽어주셔서 감사합니다.