SICP 연습문제 1.28 친절한 풀이

문제

페르마 검사가 틀린 답을 내놓지 않게 바꾼 것 가운데 밀러-라빈 검사라는게 있다. 이 검사는 페르마의 작은 정리와 달리, $n$이 소수고 $a$가 $n$보다 적고 0보다 큰 정수면 $a^{n-1}$은 1과 $modulo$ $n$으로 맞아떨어진다는 사실을 바탕으로 한다. 밀러-라빈 검사에서 어떤 수$n$이 소수인지 알려면 $a<n$인 수를 제멋대로 골라, expmod 프로시저를 써서 $a^{n-1}$ $modulo$ $n$ 을 얻는다. expmod에서 제곱을 할 때마다 ‘1 $modulo$ $n$의 뻔하지 않은 제곱근’, 곧 1이나 $n-1$은 아니면서 제곱한 값이 1 $modulo$ $n$인 수인지 알아보고 그런 1의 제곱근이 있다면 , $n$이 소수가 아님을 밝힐 수 있다. 또 $n$이 소수 아닌 홀수라면 $a<n$인 수 $a$ 가운데 적어도 반은, 이런 방법으로 $a^{n-1}$을 계산할 때 1 $modulo$ $n$의 뻔한 제곱근이 아님이 드러난다. (이런 까닭에 밀러-라빈 검사는 틀린 판단을 하지 않게 된다.) 뻔하지 않은 1의 제곱근을 찾아냈음을 알 수 있도록 expmod를 고친 다음에 fremat-test를 흉내 내어 밀러-라빈 검사 프로시저를 짜보라. 여러 소수나 소수 아닌 수를 보기 삼아 만든 프로시저가 잘 돌아가는지 시험해 보자.

문제로 부터 얻은 것

SICP는 수학적 지식을 꽤 많이 요구한다.
밀러-라빈 테스트로 페르마 테스트의 오류를 고칠 수 있다.

문제풀이

이 문제는 문제 자체를 해석하는 데에 시간이 많이 걸렸습니다.
원문으로 문제를 읽으면 이해가 약간 더 잘되지만 그래도 이해하는 데에 한참 걸렸습니다.
이해하기 쉽게 차근차근 설명해 보겠습니다.

1. 밀러-라빈 검사

밀러-라빈 검사는 $n$이 소수라면 $(1≤ a<n)$인 모든 $a$에 대해 아래의 식을 만족한다는 사실을 바탕으로 합니다.
$a^{n-1}\mod n=1$

이를 계산하기 위해서 이전 연습문제들에서 사용한 expmod 프로시저를 사용해야 합니다.

(expmod a (- n 1) n)

여기까지는 다들 이해하셨을 것이라 생각합니다.
문제는 여기서부터입니다.

2. 대체 (1 modulo n)의 뻔하지 않은 제곱근이 무엇인가?

이 단락을 완벽하게 이해하기 위해서는 아래의 정리를 숙지하고 있어야 합니다.

소수 P와 $(1≤ a\lt P)$인 어떤 $a$에 대해
($a^2 \mod P = 1$)을 만족하는 $a$는
1과 ($P-1$)밖에 없다.

한번 증명해 보겠습니다.

소수인 $P$와 $(1≤ a\lt P)$인 정수 $a$를 상정하겠습니다.
이때 ($a^2 \mod P = 1$)을 만족하는 $a$값을 찾아보겠습니다.

($a^2 \mod P = 1$)이므로,
$a^2 = Pn + 1$이 성립합니다. ($n$은 $n≥ 0$인 정수)

$a^2 = Pn + 1$에서
$Pn = a^2 - 1 = (a-1)(a+1)$

$P$는 소수이므로, n이 0이 아니라면 $P$는 무조건 $(a-1),(a+1)$ 둘 중에 하나입니다.
이때 $(a\lt P)$이므로 $P=(a+1)$입니다.

정리하자면, ($a^2 \mod P = 1$)이 성립하기 위해서는
$a$는 $1$이거나 $(P-1)$이어야 하는 것입니다.

다시 돌아가서, (1 modulo n)의 뻔하지 않은 제곱근이란,
$a=1$이거나 $a=n-1$이 아님에도 불구하고, ($a^2 \mod n = 1$)을 만족하는 $a$를 말합니다.
그리고 이런 $a$가 존재한다면, n은 소수가 아닌 것입니다.

이 증명 과정을 책에서는 생략했기 때문에, 문제 이해가 극도로 어려웠습니다.

3. expmod 프로시저 살펴보기

지금까지 사용한 expmod 프로시저는 다음과 같습니다.
(혹시라도 expmod의 원리가 궁금하시다면 이 글을 봐주시기 바랍니다.)

(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (remainder (square (expmod base (/ exp 2) m))
                    m))
        (else
         (remainder (* base (expmod base (- exp 1) m))
                    m))))

여기서 주목할 점은, 프로시저가 square를 포함한다는 것입니다.

(remainder (square (expmod base (/ exp 2) m)) m)

위 과정에서 expmod의 결과가 (1 modulo m)의 뻔하지 않은 제곱근이라면, 더 계산할 것도 없이 m은 소수가 아닙니다.
그러므로 square 연산을 하기 전에 뻔하지 않은 제곱근 검사를 하면, 계산과정을 단축시킬 수 있습니다.

(define (nontrivial-test x m)
  (if (and (not (= x 1))
           (not (= x (- m 1)))
           (= (remainder (square x) m) 1))
      0
      (remainder (square x) m)))

위의 프로시저를 써서 expmod를 새로 쓰면 다음과 같습니다.

(define (nontrivial-test x m)
  (if (and (not (= x 1))
           (not (= x (- m 1)))
           (= (remainder (square x) m) 1))
      0
      (remainder (square x) m)))
    
(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (nontrivial-test (expmod base (/ exp 2) m)
                    m))
        (else
         (remainder (* base (expmod base (- exp 1) m))
                    m))))

4. prime? 실행해보기

이제 밀러-라빈 검사를 기반으로 prime? 프로시저를 만들어 보겠습니다.

(define (square x)
  (* x x))

(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (nontrivial-test (expmod base (/ exp 2) m)
                    m))
        (else
         (remainder (* base (expmod base (- exp 1) m))
                    m))))

(define (nontrivial-test x m)
  (if (and (not (= x 1))
           (not (= x (- m 1)))
           (= (remainder (square x) m) 1))
      0
      (remainder (square x) m)))

(define (miller-rabin-test n)
  (define (try-it a)
    (= (expmod a (- n 1) n) 1))
  (try-it (+ 1 (random (- n 1)))))

(define (prime? n times)
  (cond ((= times 0) true)
        ((miller-rabin-test n) (prime? n (- times 1)))
        (else false)))

그리고 카마이클 수를 포함한 여러 수를 테스트해 보겠습니다.

(prime? 7 100)
(prime? 11 100)
(prime? 12 100)
(prime? 561 100)  
(prime? 1105 100)

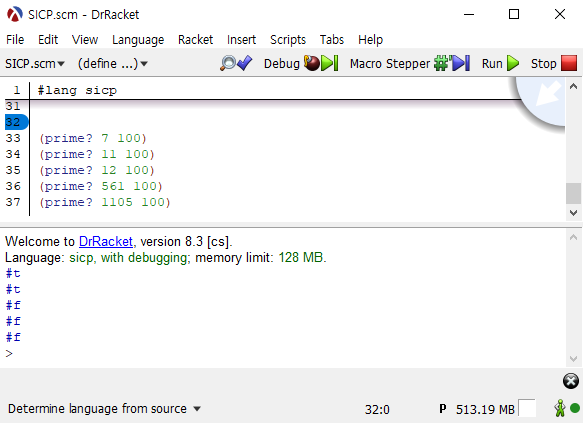
카마이클 수도 소수로 판정하지 않고 #f를 반환하는 모습입니다.

긴 글 읽어주셔서 감사합니다.