SICP 연습문제 1.29 친절한 풀이

문제

심슨의 규칙은 위 방법보다 더 정확하게 적분 값을 구할 수 있는 방법이다.
이 규칙에 따라 a에서 b 사이에서 함수 f를 정적분한 값에 가까운 값은 다음처럼 어림잡는다.

$\frac{h}{3}[y$₀$+4y$₁$+2y$₂$+4y$₃$+2y$₄$+⋯+2y$_$n-2$$+4y$_$n-1$$+y$_$n$$]$

위 식에서 $n$이 짝수일 때 $h=(b-a)/n$이고, $y$_$k$$=f(a+kh)$이다. ($n$이 커질수록 조금씩 정답에 다가간다.) $f, a, b$를 인자로 받아서 심슨의 규칙으로 정적분값을 얻는 프로시저를 짜보라. 그런 다음, 그 프로시저로 ($n=100,n=1000$인 경우) 0부터 1사이에서 cube를 정적분한 값을 얻고, 그 값을 앞서 integral 프로시저로 얻은 것과 견주어 보라.

문제로 부터 얻은 것

차수 높은 프로시저로 요악하는 법을 연습할 수 있는 문제였습니다.

문제풀이

이 문제를 해결하기 위해서는 앞의 절인 1.3.1절의 sum과 integral을 잘 이해하고 있어야 합니다.

1. sum 프로시저

sum 프로시저부터 살펴보겠습니다.

(define (sum term a next b)
  (if (> a b)
      0
      (+ (sum term (next a) next b)
         (term a))))

이 프로시저의 특이한 점은 프로시저를 인수로 받는다는 것입니다.
인수인 term과 next의 자리에는 데이터가 아닌 프로시저가 옵니다.

term과 next의 역할은 프로시저의 내부를 보면 알 수 있습니다.
sum이 반환하는 값은 결론적으로 (term a)들의 합입니다.
이때 a값이 순차적으로 변하는 규칙을 명시한 것이 next라고 볼 수 있습니다.

예시로 아래의 예는 $x$가 1~5일때 $x^2$의 합을 나타낸 과정입니다.

(define (square x)
  (* x x))

(define (next n)
  (+ n 1))

(sum square 1 next 5) #55

$1^2+2^2+3^2+4^2+5^2=55$

2. integral 프로시저

integral 프로시저는 sum 프로시저를 이용해서 만든 정적분 프로시저입니다.

(define (integral f a b dx)
  (define (add-dx x)
    (+ x dx))
  (* (sum f (+ a (/ dx 2.0)) add-dx b)
     dx))

위의 프로시저에서 눈여겨볼 점은 a자리에 (+ a (/ dx 2.0)이 들어간다는 것입니다.
위의 프로시저를 이해하기 위해 $x^2$함수의 경우를 생각해 보겠습니다.

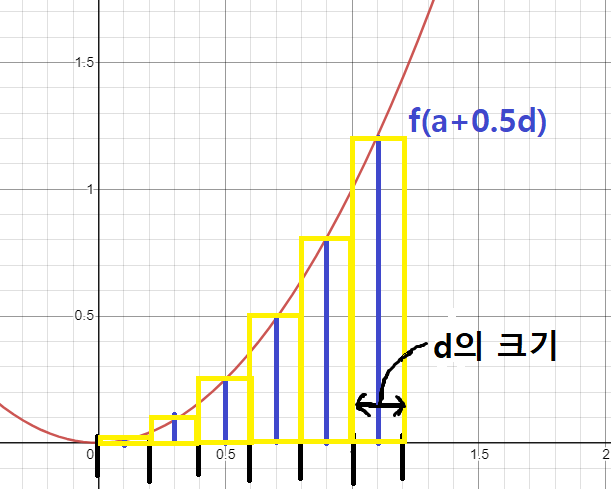
위의 그래프에서 파란색 선의 길이는 각각 $f(a+0.5dx)$, $f(a+1.5dx)$, $f(a+2.5dx), ⋯$를 계산한 값을 의미합니다.
그 길이의 합에 dx를 곱하게 되면, 최종적으로 프로시저의 결과는 노란색 사각형들의 넓이의 합이 됩니다.
노란색 사각형들의 넓이의 합은 얼추 정적분값과 비슷해집니다.

3. 심슨 규칙에 따라 정적분 프로시저 만들기

저는 아래와 같이 심슨 규칙을 프로시저화 했습니다.
$\frac{h}{3}[y$₀$+4y$₁$+2y$₂$+4y$₃$+2y$₄$+⋯+2y$_$n-2$$+4y$_$n-1$$+y$_$n$$]$

(define (simpson-rule f a b n)
  (define (next x)
    (+ x 1))
  (define h
    (/ (- b a) n))
  (define (y k)
    (f (+ a (* k h))))
  (define (term k)
    (cond ((= k 0) (y 0))
          ((= k n) (y n))
          ((even? k) (* (y k) 2))
          (else (* (y k) 4))))
  
  (* (/ h 3)
     (sum term 0 next n)))

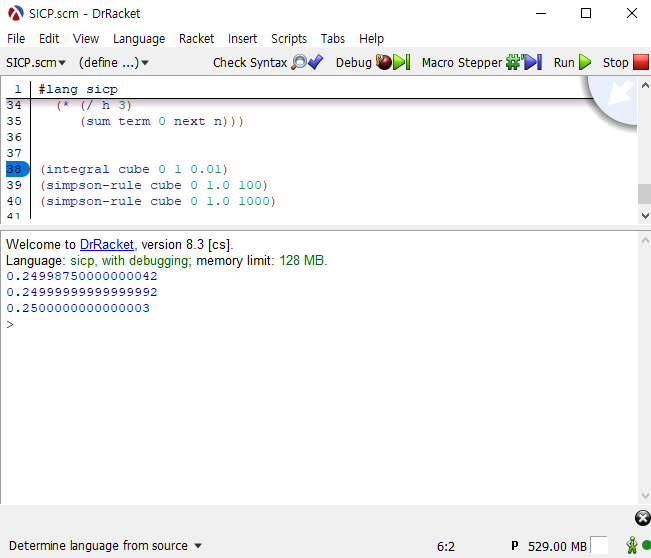
그리고 문제의 요구사항대로 아래의 식을 실행했습니다.

(integral cube 0 1 0.01)
(simpson-rule cube 0 1.0 100)
(simpson-rule cube 0 1.0 1000)

심슨 규칙은 기존의 인테그랄에 비해 더 정확한 적분을 하는 것을 볼 수 있습니다.

읽어주셔서 감사합니다.