SICP 연습문제 1.35 친절한 풀이

문제

1.2.2절에 나온 황금비 $ϕ$가 $x \mapsto 1+1/x$ 함수의 고정점이라는 것을 밝히고, 이런 사실을 바탕으로 fixed-point 프로시저로 $ϕ$를 찾아보라.

문제로 부터 얻은 것

고정점 찾기를 프로시저로 작성해볼 수 있는 시간이었습니다.
let의 사용에 익숙해질 수 있었습니다.

문제풀이

고정점에 대한 이해는 1.3.3절에서 충분히 했다고 생각합니다.
고정점이란 결국 $f(x)=x$인 $x$를 찾는 것입니다.

아래의 식을 풀어보겠습니다.
$f(x)=1+1/x$
$x=1+1/x$
$x^2=x+1$
$x^2-x-1=0$
$x=\frac{1+\sqrt{5}}{2}=ϕ$

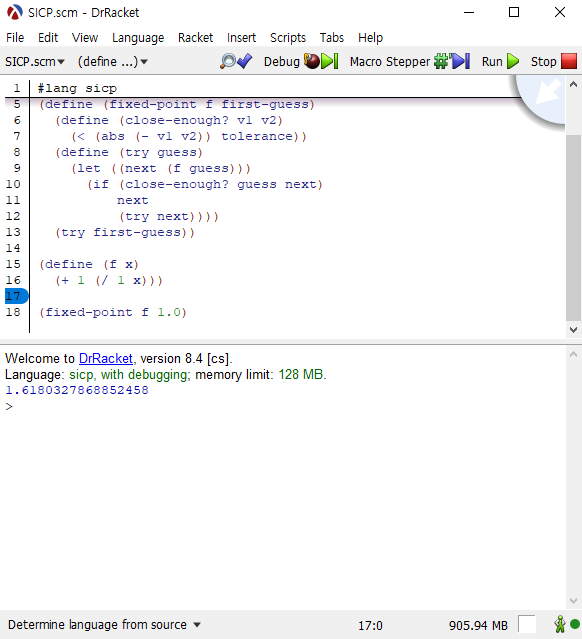
fixed-point 프로시저로 정확한 값을 알아보겠습니다.

(define tolerance 0.00001)

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

(define (f x)
  (+ 1 (/ 1 x)))

(fixed-point f 1.0)

읽어주셔서 감사합니다.