SICP 연습문제 1.36 친절한 풀이

문제

연습문제 1.22에서 나온 기본 프로시저 newline과 display를 써서 이어지는 어림값을 찍어내도록 fixed-point를 고쳐 보라. 그리고 $x \mapsto \log(1000)/\log(x)$의 고정점을 찾아서 $x^x=1000$에 맞는 x값을 얻어라. (귀띔:Scheme의 기본 프로시저 log를 쓰면 자연 로그 값을 얻을 수 있다. 함수 값의 평균을 내어 잦아들 때와 그냥 놔둘 때 계산 단계를 얼마나 거치는지 알아보라. (귀띔:이 문제에서 첫 어림값이 1이면 $\log(1)=0$을 분모로 하는 나눗셈이 필요하므로 1은 첫 어림값이 되지 못한다.)

문제로 부터 얻은 것

고정점 찾기 프로시저를 이해하는 것 외에 크게 문제의 의미는 없어보입니다.

문제풀이

1. fixed-point 수정

(display guess), (newline)을 추가했습니다.

(define tolerance 0.00001)

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (display guess)
      (newline)
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

2. 고정점 찾기

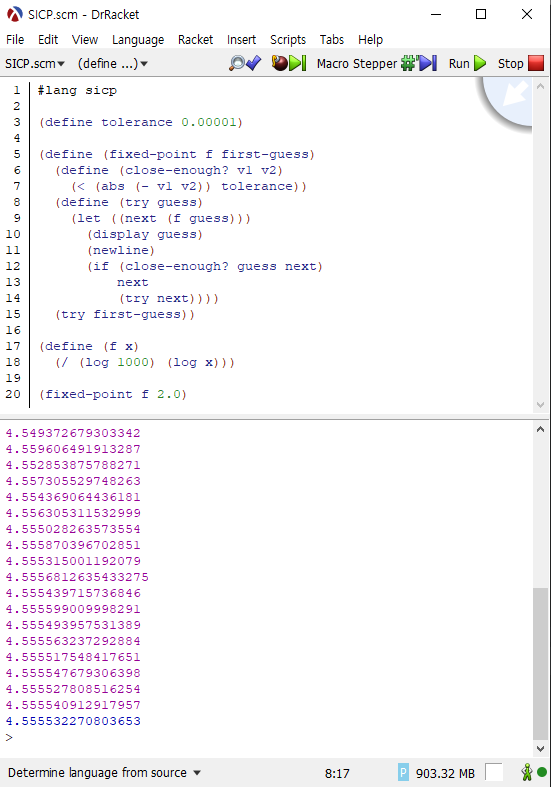
아래의 프로시저를 실행해 보았습니다.

(define (f x)
  (/ (log 1000) (log x)))

(fixed-point f 2.0)

읽어주셔서 감사합니다.