SICP 연습문제 1.37 친절한 풀이

문제

다음 꼴로 쓴 수식을 끝없는 연속분수^{continued fraction}라 한다.

$f=\frac{N_{1}}{D_{1} + \frac{N_{2}}{D_{2}+\frac{N_{3}}{D_{3}+⋯}}}$

이를테면 $N_{i}$와 $D_{i}$가 1일때 위 분수를 펼치면 $1/ϕ$에 다가간다. ($ϕ$는 1.2.2절에서 나온 황금비다.) 계속 나눈 수 값을 어림잡을 때 다음처럼 정해 둔 마디 몇개만 펼치고 나머지 마디는 잘라내는 방법을 쓸 수 있다. 이를 두고 k-마디로 끝나는 연속분수라 한다.

$f=\frac{N_{1}}{D_{1}+\frac{N_{2}}{⋱+\frac{N_{k}}{D_{k}}}}$

분수에서 (마디 번호 i를 인자로 받아) $N\scriptscriptstyle{i}$와 $D\scriptscriptstyle{i}$값을 계산하는 프로시저를 n과 d라고 하자. k-마디로 끝나는 연속분수 값을 (cont-frac n d k)로 계산할 수 있도록 프로시저 cont-frac을 정의하라. 프로시저가 올바로 움직이는지 살펴보기 위해서, k값을 조금씩 늘려가며 아래 식으로 $1/ϕ$에 가까운 값을 얻어내는 실험을 하자.

(cont-frac (lambda (i) 1.0)
           (lambda (i) 1.0)
           k)

k값이 얼마나 커야 소수점 아래 4자리까지 맞아떨어지는 값을 어림잡을 수 있는가?

b. cont-frac 프로시저의 프로세스가 되돈다면 반복하게끔 고쳐 쓰고, 그 반대로 반복한다면 되돌게끔 고쳐라.

문제로 부터 얻은 것

경험해 보지 못한 방식의 반복을 프로시저로 구현하면서 사고력을 얻을 수 있었습니다.

문제풀이

a. 1/ϕ구하기

cont-frac 프로시저를 구현하는 것은 어렵지 않았습니다.
무지성으로 문제의 식을 코드로 바꾸다 보니 해결되었습니다.

$\frac{N}{D + iter}$

(/ (n i) (+ (d i) (iter (+ i 1))))

cont-frac 프로시저를 구현하면 아래와 같습니다.

(define (cont-frac n d k)
  (define (iter i)
    (if (= i k)
        (/ (n i) (d i))
        (/ (n i) (+ (d i) (iter (+ i 1))))))
  (iter 1))

위 프로시저를 바탕으로 아래의 식을 실행해 보겠습니다.

(cont-frac (lambda (i) 1.0)
           (lambda (i) 1.0)
           10000)  

구글 계산기로 계산한 $1/ϕ$는 0.61803398876입니다.
문제에서 요구하는 소수점아래 4자리까지 맞아 떨어지는 반복횟수를 구하기 위해 아래의 프로시저를 실행시켜 보았습니다.

(define (iter n)
  (define (try k)
    (cont-frac (lambda (i) 1.0)
               (lambda (i) 1.0)
               k))
  (define (goodenough? x)
    (< (abs (- x 0.61803398876)) 0.0001))
  (if (goodenough? (try n))
      (display n)
      (iter (+ n 1))))

(iter 1)

결과로는 10을 반환했습니다.
그런데 goodenough?를 통과했다고 해서 소수점 4자리까지 맞아 떨어지지는 않았습니다.

10 언저리의 숫자들로 테스트해보니,
소수점아래 4자리까지 맞아 떨어지는 반복횟수는 11이었습니다.

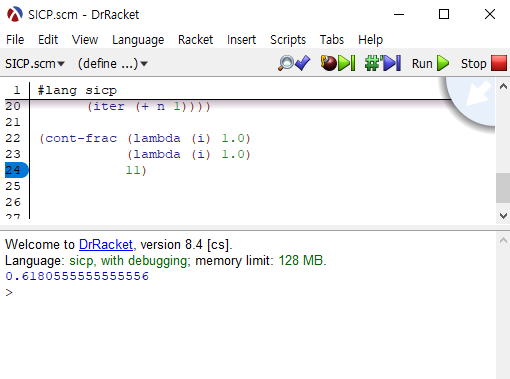
b. cont-frac를 반복하는 프로세스로 구현하기

cont-frac을 반복하는 프로세스로 구현하기 위해서 기존의 아이디어와는 다른 아이디어를 떠올렸습니다.
1부터 k까지 반복하는 것이 아닌, k부터 1까지 역순으로 반복하는 것입니다.
그리고 그 계산값을 아래와 같이 result에 축적하는 것입니다.
$result \longleftarrow \frac{N}{D+result}$ (result의 초기값은 0)

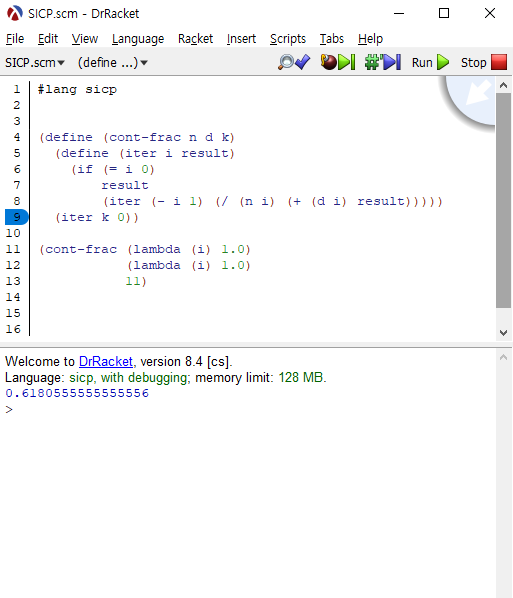
프로시저로 구현하면 아래와 같습니다.

(define (cont-frac n d k)
  (define (iter i result)
    (if (= i 0)
        result
        (iter (- i 1) (/ (n i) (+ (d i) result)))))
  (iter k 0))

읽어주셔서 감사합니다.