SICP 연습문제 1.38 친절한 풀이

문제

1737년에 스위스의 수학자 레온하르트 오일러가 De Fractionibus Continuis라는 논문을 출판하였는데, 그 논문에서 $e-2$로 펼쳐지는 연속 분수가 나왔다. 여기서 $e$는 자연로그의 밑수다. 이 분수에서 모든 $N$_$i$는 1이고, $D$_$i$는 차례로 1,2,1,1,4,1,1,6,1,1,8$⋯$가 된다. 이 방법에 바탕을 두고, 연습문제 1.37에서 작성한 cont-frac 프로시저를 사용하여 $e$를 추정하는 프로그램을 짜라.

문제로 부터 얻은 것

수열의 규칙을 식으로 옮기는 연습이 되는 문제였습니다.

문제풀이

이 문제의 핵심은 $D$_$i$의 규칙을 프로시저로 나타내는 것입니다.
저는 (n mod 3=2)에서 값이 $\frac{2(n+1)}{3}$인 것을 확인하고 (D n)프로시저를 작성했습니다.

(define (D n)
  (if (= (remainder n 3) 2)
      (* 2 (/ (+ n 1) 3))
      1))

위 프로시저를 기반으로 $e$를 구해보겠습니다.
(cont-frac 프로시저는 연습문제 1.37에 있습니다.)

(define (D n)
  (if (= (remainder n 3) 2)
      (* 2 (/ (+ n 1) 3))
      1))

(define e
  (+ 2
     (cont-frac (lambda (i) 1.0)
                D 
                100000)))

(display e)

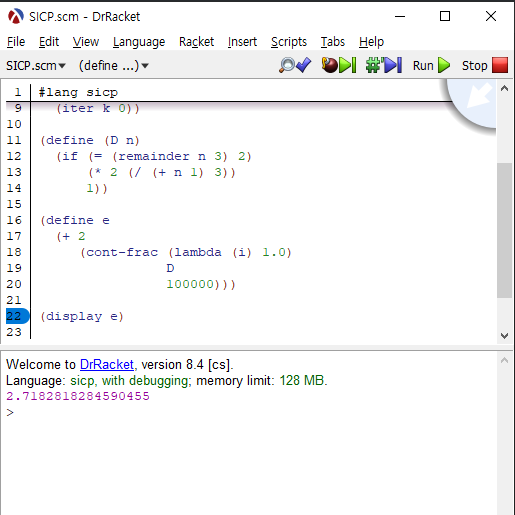
구글 계산기 기준으로 $e$는 2.71828182846입니다.
상당히 근접한 값을 찾아냈습니다.

읽어주셔서 감사합니다.