SICP 연습문제 1.39 친절한 풀이

문제

탄센트 함수를 연속 분수로 나타내면 다음과 같다. 이 정의는 독일의 수학자 요하네스 하인리히 람베르트가 1770년에 발표한 것이다.

$\tan{x}=\frac{x}{1-\frac{x^2}{3-\frac{x^2}{5-⋱}}}$

여기에서 $x$는 라디안 값이다. 람베르트 식으로 탄젠트 함수 값에 가까운 값을 구하는 프로시저 (tan-cf x k)를 정의하라. 여기서 k는 연습문제 1.37에서과 마찬가지로 계산에 쓸 마디 수를 나타낸다.

문제로 부터 얻은 것

저번 문제와 동일하게 수열의 규칙을 프로시저로 옮기는 데에 도움이 되는 문제였습니다.

문제풀이

문제 해결을 위해서 연습문제 1.37의 cont-frac 프로시저를 사용하겠습니다.

아래는 원본 cont-frac 프로시저입니다.

(define (cont-frac n d k)
  (define (iter i)
    (if (= i k)
        (/ (n i) (d i))
        (/ (n i) (+ (d i) (iter (+ i 1))))))
  (iter 1))

N과 D는 다음과 같이 설계했습니다.
N은 x값을 포함해야 하기 때문에 (N n x)로 만들었습니다. 또한, k가 1이 아닌 경우에 $x^2$를 반환하도록 하였습니다.
D는 $1,3,5,7,9,⋯$를 표현하였습니다.

(define (N n x)
  (if (= n 1)
      x
      (square x)))

(define (D n)
  (- (* n 2) 1))

새로운 N과 D에 맞게 cont-frac도 변형하였습니다.
기존의 프로시저에서 +가 -로 바뀌고, x 인자를 받도록 변형하였습니다.

(define (cont-frac n d k x)
  (define (iter i)
    (if (= i k)
        (/ (n i x) (d i))
        (/ (n i x) (- (d i) (iter (+ i 1))))))
  (iter 1))

위 프로시저들을 기반으로 구현한 tan-cf 프로시저입니다.

(define (square x)
  (* x x))

(define (cont-frac n d k x)
  (define (iter i)
    (if (= i k)
        (/ (n i x) (d i))
        (/ (n i x) (- (d i) (iter (+ i 1))))))
  (iter 1))

(define (N n x)
  (if (= n 1)
      x
      (square x)))

(define (D n)
  (- (* n 2) 1))

(define (tan-cf x k)
  (cont-frac N D k x))

이 프로시저가 정상작동하는지 확인하기 위해 $\frac{π}{4}$를 인자로 넘겨보겠습니다.
$\frac{π}{4}=\frac{3.14}{4}=0.785$

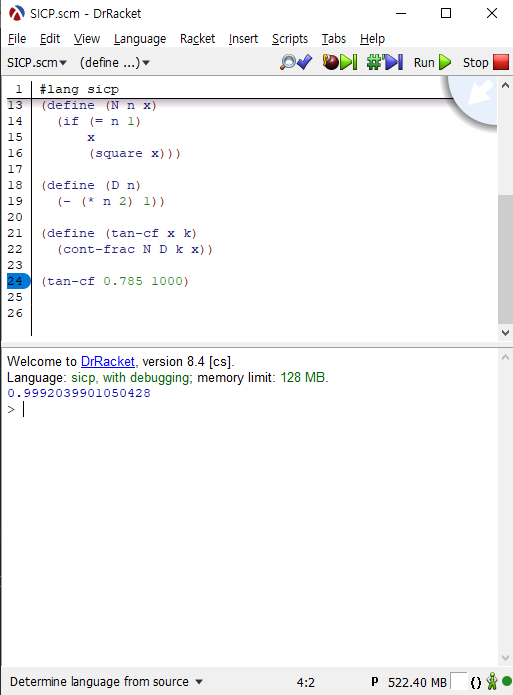
tan(π/4)를 1에 가깝게 계산하므로 본 프로시저는 옳은 프로시저라 할 수 있습니다.

읽어주셔서 감사합니다.