SICP 연습문제 1.40 친절한 풀이

문제

삼차 방정식 $x^3+ax^2+bx+c$의 해에 가까운 값을 구하기 위하여 newtons-method로 다음 식을 계산한다고 할 때, 이 식에서 쓰는 프로시저 cubic을 짜보라.

(newtons-method (cubic a b c) 1)

문제로 부터 얻은 것

newtons-method에 사용된 프로시저들을 다시 되짚어보기 위한 문제였습니다.

문제풀이

이 문제를 단순히 푸는 것은 그렇게 중요하지 않습니다.
다만 중요한 것은, newtons-method의 원리를 이해하고 가는 것입니다.

newtons-method를 이해하기 위해서는 아래의 식들을 이해해야 합니다.
여기서 이해한다는 것은, 약간의 수학적인 이해와 더불어 어떻게 구현하는지를 이해하는 것입니다.
우리는 컴퓨터공학도지 수학도가 아닙니다.

a. 미분 프로시저

$dg(x)=\frac{g(x+dx)-g(x)}{dx}$ ($dx$는 매우 작은 값)

(define (deriv g)
  (define dx 0.00001)
  (lambda (x)
    (/ (- (g (+ x dx)) (g x))
       dx)))

b. 고정점 프로시저

$f(x)=x$를 만족하는 $x$는
추정값인 guess에 대해 $f(f(f(f⋯ f(guess))))$의 값과 같다.

(define tolerance 0.00001)

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

c. 뉴턴법

미분 가능한 함수 $g(x)$에 대해
$g(x)=0$의 해는
$f(x)=x-\frac{g(x)}{dg(x)}$의 고정점 즉,
$x=x-\frac{g(x)}{dg(x)}$의 해와 같다.

이를 구현하기 위해 newton-transform 프로시저를 따로 정의한다.

(define (newtons-transform g)
  (lambda (x)
    (- x (/ (g x) ((deriv g) x)))))

(define (newtons-method g guess)
  (fixed-point (newtons-transform g) guess))

d. 삼차방정식의 해 구하기

(newtons-method g guess)는 결국 g식의 해를 구하는 프로시저입니다.
문제에서 요구하는 cubic 프로시저는 아래와 같습니다.
$cubic(x)=x^3+ax^2+bx+c$

(define (cubic a b c)
  (lambda (x)
    (+ (cube x)
       (* a (square x))
       (* b x)
       c
       )))

만든 프로시저를 시험하기 위해 아래의 식을 실행시켜 보겠습니다.
$(x+4)(x+2)(x-8)=x^3-2x^2-40x-64$

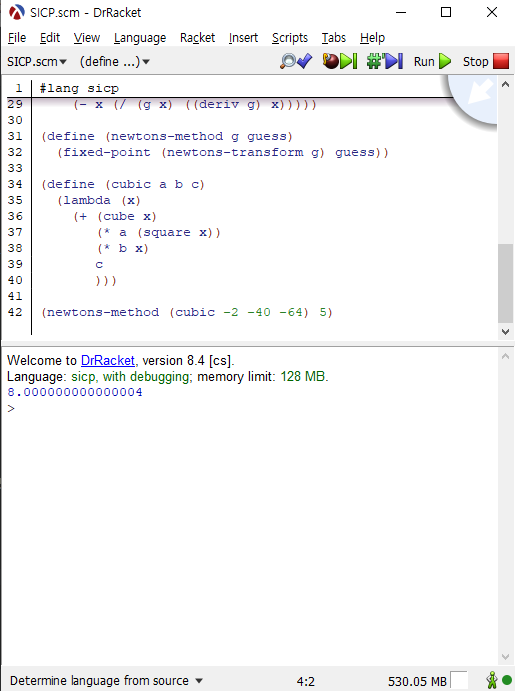
(newtons-method (cubic -2 -40 -64) 5)

읽어주셔서 감사합니다.