SICP 연습문제 1.41 친절한 풀이

문제

인자 하나 받는 프로시저를 인자로 받아, 그 프로시저를 두번 연거푸 계산하는 프로시저를 내놓도록, 프로시저 double을 짜 보자. 예컨데, inc가 인자에 1을 더하는 프로시저라면 (double inc)는 2를 더하는 프로시저가 된다. 다음 식의 값은 얼마인가?

(((double (double double)) inc) 5)

문제로 부터 얻은 것

((a b) x) = (a (b x))가 항상 성립하지는 않습니다.
함수끼리 연산된 함수에 값을 입력하는 경우에는, 함수를 먼저 정확히 계산해 주어야 합니다.

문제풀이

이문제의 풀이는 꼭꼭 씹어드셔야 이해하기 쉽습니다.
한줄 한줄 씹어먹어 주시기 바랍니다.

처음 이 문제를 봤을때, 단순한 저의 생각은 아래와 같았습니다.

double이 두번 실행하는 것이라면,
(double double)은 네번 실행하는 것이고,
(double (double double))은 여덟번 실행하는 것이므로,
(((double (double double)) inc) 5) = 5+8 =13이 아닐까?

시간을 들여서 깊게 고민해 보았습니다.
하지만 만족스러운 결론을 얻지 못했습니다.
차선책으로, 아래의 코드를 실행시켜서 사고의 힌트를 얻고자 했습니다.
편의를 위해서 double은 d로 치환하였습니다.

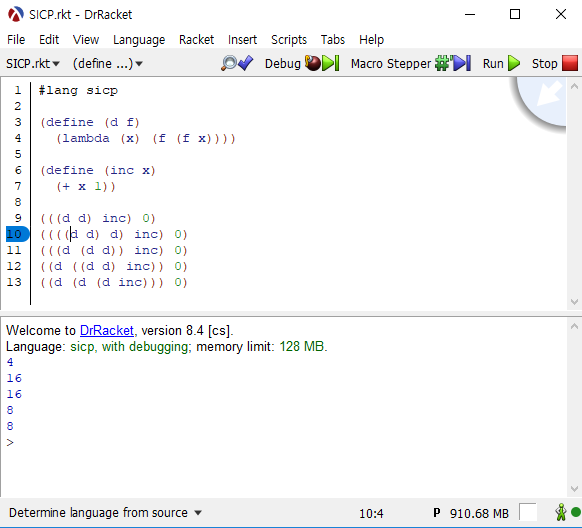
위 실험에서 제가 주목한 부분은 아래의 두 식입니다.
(d ((d d) inc)) = (lambda (x) (+ x 8))
((d (d d)) inc) = (lambda (x) (+ x 16))
괄호를 어떻게 묶느냐에 따라서 결과가 달라진다는 것을 보여준 결과입니다.

위의 결과에서 깨달은 중요한 사실이 있습니다.
제가 은연중에 아래의 식을 당연하게 생각하고 있었다는 것입니다.
((d (d d)) f) = (d ((d d) f))

즉, 람다함수 a b에 대해
((a b) f) = (a (b f))가 성립한다고 당연하게 생각하고 있었던 것입니다.

그 생각은 당연히 틀렸습니다.

((d (d d)) f)식을 제대로 정리하면 다음과 같습니다.

(d (d d))
= (lambda (x) ((d d) ((d d) x)))
위의 식은 (d f)의 정의에 맞게 f 인자에 (d d)를 넣은 결과입니다.

((d (d d)) f)
= ((lambda (x) ((d d) ((d d) x))) f)
= ((d d) ((d d) f))

((d (d d)) f)
= ((d d) ((d d) f))

(d f) = (lambda (x) (f (f x)))이므로,
(d d) = (lambda (x) (d (d x)))입니다.
((d d) f) = (d (d f))

((d (d d)) f)
= ((d d) ((d d) f))
= (d (d ((d d) f)))
= (d (d (d (d f))))

((d (d d)) inc)
= (d (d (d (d inc))))
= (lambda (x) (+ x 16))

함수끼리 연산된 함수에 값을 입력하는 경우에는, 함수를 먼저 정확히 계산해 주어야 합니다.
난해한 글 읽어주셔서 감사합니다.