SICP 연습문제 1.45 친절한 풀이

문제

1.3.3절에서 곧바로 $y\mapsto x/y$ 함수의 고정점을 얻으려고 할 때 함수 값이 고정점에 다가가지 못하고 들쑥날쑥해서, 이 값을 평균내어 잠재워서 풀었다. 이와 비슷하게, $y\mapsto x/y^2$ 함수의 고정점을 구하여 세제곱근을 계산할 때에도 평균내어 잦아들게 할 수 있다. 하지만, 네제곱근은 이렇게 되지 않는다. 다시 말해서, $y\mapsto x/y^3$ 함수는 평균 잠재우기를 한 번 써봤자 고정점으로 다가가지 않는다. 그런데, 두 번 하면, 다시 말해서 평균내어 잦아들게 한 것을 다시 한번 더 평균내어 잦아들게 하면 고정점에 다가간다. $y\mapsto x/y^{n-1}$을 평균내어 여러 번 잦아들게 하여 고정점 찾기로 n번째 제곱근을 구한다고 할 때, 몇 번 잦아들게 하는지 실험으로 알아보라. 이를 바탕으로 fixed-point, average-damp, 연습문제 1.43의 repeated를 써서 n번째 제곱근을 얻는 프로시저를 만들어 보자. 이 프로시저를 만드는 과정에서 꼭 필요한 수 연산은 모두 기본 연산이라고 해두자.

문제로 부터 얻은 것

이전에 배운 개념들을 전부 조합해야 풀 수 있는 문제입니다.
자신이 어느 부분에서 이해가 부족했는지를 점검할 수 있었습니다.

문제풀이

1. 선행지식

1장의 최종 문제 둘중 하나 답게 여태까지 배운 여러가지 개념들을 이해하고 사용해야 하는 문제입니다.
이 문제를 풀기 위해 이해해야 하는 개념들은 다음과 같습니다.

a. 고정점 프로시저

$f(x)$의 고정점은 $f(f(f(⋯ f(guess)))$와 같습니다.

(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

b. average-damp

고정점 찾기 문제에서 f 함수를 반복해서 연산하면 값이 고정점에 다가가지 못하고 들쑥날쑥하는 경우가 있습니다.
이때, f 함수 연산을 반복하는 대신에 $\frac{f(x)+x}{2}$ 즉 (average-damp f) 연산을 반복하면 이 문제를 해결할 수 있는 경우가 있습니다.

(define (average-damp f)
  (lambda (x) (/ (+ (f x) x) 2)))

c. fast-exp

(fast-exp b n)=$b^n$ 너무 오래되어서 기억나지 않으실까봐 넣어 놨습니다.

(define (exp-iter b n temp)
  (cond ((= n 0) temp)
        ((even? n) (exp-iter (square b) (halves n) temp))
        (else (exp-iter b (- n 1) (* temp b)))))

(define (fast-exp b n)
  (exp-iter b n 1))

d. compose & repeated

바로 전 문제에서 연습했던 것들이니 크게 설명은 필요하지 않을 것 같습니다.

(define (compose f g)
  (lambda (x) (f (g x))))

(define (repeated f n)
  (if (= n 1)
      f
      (compose f (repeated f (- n 1)))))

2. n번째 제곱근을 위한 평균 잠재우기 횟수

평균 잠재우기를 n번 시행한다는 말은 다음과 같습니다.

$\frac{(f(x) + x)}{2}=AV1$
$\frac{(f(AV1) + AV1)}{2}=AV2$
$\frac{(f(AV2) + AV2)}{2}=AV3$
$⋯$
$\frac{(f(AV{n-1}) + AV{n-1})}{2}=AVn$

이를 프로시저로 나타내면 다음과 같습니다.

(define (average-damp-n f n)
  (repeated (average-damp f) n))

(average-damp-n f n)을 fixed-point 프로시저에 적용시키면 다음과 같습니다.
damp-number 인자로 평균 잠재우기 횟수를 넘겨주었습니다

(define (fixed-point f first-guess damp-number)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next ((average-damp-n f damp-number) guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

그리고 아래의 프로시저를 구상했습니다.
damp 횟수를 인자로 받아서 그만큼 평균갑 잠재우기를 실행한 fixed-point를 사용한 n의 제곱근을 구하는 프로시저입니다.

(define (nth-root n damp-number)
  (define (f x)
    (lambda (y) (/ x (fast-exp y (- n 1)))))
  (lambda (x)
    (fixed-point (f x) 1.0 damp-number)))

이 프로시저로 실험을 해보니 n의 제곱근을 구하기 위해서는,
최소 [log₂n]만큼의 평균값 잠재우기를 해야 한다는 것을 알아냈습니다.
[x]는 x보다 작은 최대의 정수값입니다.

3. n번째 제곱근 구하기 프로시저

위의 실험결과를 바탕으로 아래의 프로시저를 구상했습니다.
(log a b)=log_ba
(floor x)는 x보다 작은 최대의 정수

(define (nth-root n)
  (define damp-number
    (floor (log n 2)))
  (define (f x)
    (lambda (y) (/ x (fast-exp y (- n 1)))))
  (lambda (x)
    (fixed-point (f x) 1.0 damp-number)))

그리고 시험을 위해 아래의 테스트 코드를 실행해 보았습니다.

((nth-root 2) 100)
((nth-root 3) 1000)
((nth-root 4) 10000)
((nth-root 5) 100000)
((nth-root 6) 1000000)
((nth-root 7) 10000000)
((nth-root 8) 100000000)
((nth-root 9) 1000000000)

결과는 다음과 같았습니다.

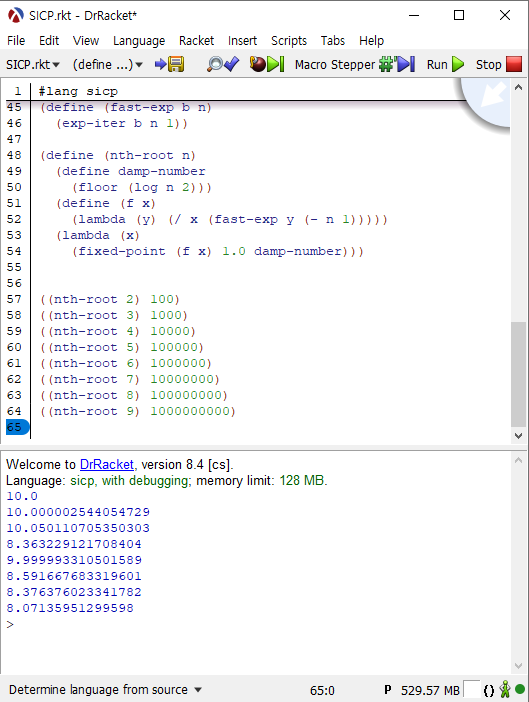
프로시저가 예상한 결과대로 작동한다면 모든 식의 답이 10이어야겠지만, 그렇지는 않았습니다.

긴 글 읽어주셔서 감사합니다.