SICP 연습문제 1.46 친절한 풀이

문제

이 장에서 설명한 여러 수 계산법은 반복하여 고치기라 하는 더 일반적인 방법에 바탕을 둔다. 무엇을 반복해서 고친다는 말은 이런 뜻이다. 어떤 값을 얻고자 할 때, 처음에 그 값을 어림잡은 어떤 값에서 시작하되 어떤 계산과정을 거쳐서 더 나은 어림값을 만든다. 꽤 쓸 만한 어림값이 나올 때까지 그 계산과정을 되풀이한다. 이런 일반적인 방법을 곧바로 나타내는 iterative-improve 프로시저를 짜보자. 이 프로시저는 어림값이 충분히 괜찮은지 알아보는 방법과 더 좋은 어림값을 계산하는 방법을 프로시저 인자로 받아서, 무언가를 반복하여 고치는 프로시저를 결과 값으로 내놓는다. 1.1.7절의 sqrt 프로시저와 1.3.3절의 fixed-point 프로시저가 iterative-improove를 쓰도록 고쳐보라.

문제로 부터 얻은 것

1장의 제목은 프로시저를 써서 요약하기입니다.
1장의 마지막 문제에서 지금까지 배운 개념들의 정수를 프로시저를 써서 요약했습니다.
코드의 표현력을 끌어올리는 연습이 잘 된것 같아 좋습니다.

문제풀이

1단원 내내 반복한 형태이기 때문에, 코드를 짜는 것은 그렇게 어렵지 않았습니다.

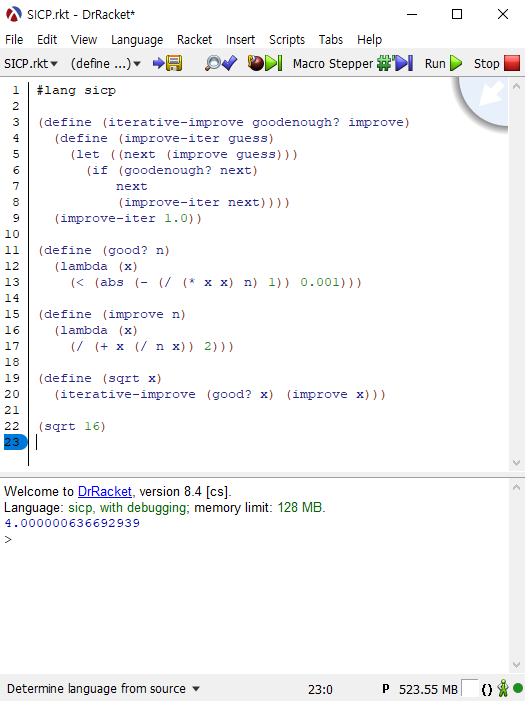
(define (iterative-improve goodenough? improve)
  (define (improve-iter guess)
    (let ((next (improve guess)))
      (if (goodenough? next)
          next
          (improve-iter next))))
  (improve-iter 1.0))

a. sqrt 프로시저 구현하기

구현한 sqrt는 아래와 같습니다.

(define (good? n)
  (lambda (x)
    (< (abs (- (/ (* x x) n) 1)) 0.001)))

(define (improve n)
  (lambda (x)
    (/ (+ x (/ n x)) 2)))

(define (sqrt x)
  (iterative-improve (good? x) (improve x)))

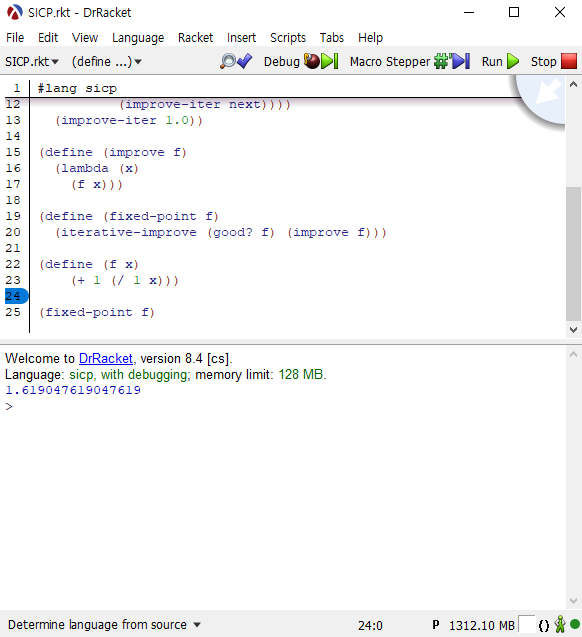
b. fixed-point 구현하기

구현한 fixed-point는 다음과 같습니다.

(define (good? f)
  (lambda (x)
    (< (abs (- (/ (f x) x) 1)) 0.001)))

(define (improve f)
  (lambda (x)
    (f x)))

(define (fixed-point f)
  (iterative-improve (good? f) (improve f)))

동작을 확인하기 위해 연습문제 1.35의 예시를 활용했습니다.
황금비 $ϕ$는 $x\mapsto{1+1/x}$의 고정점값인, 1.618…입니다.

(define (f x)
    (+ 1 (/ 1 x)))

(fixed-point f)

1장의 제목은 프로시저를 써서 요약하기입니다.
1장의 마지막 문제에서 지금까지 배운 개념들의 정수를 프로시저를 써서 요약했습니다.
코드의 표현력을 끌어올리는 연습이 잘 된것 같아 좋습니다.

읽어주셔서 감사합니다.