SICP 연습문제 1.7 친절한 풀이

문제

앞서 만든 goodenough?로는 아주 작은 수의 제곱근을 구하지 못한다. 또 컴퓨터에서 수를 셈할 때에는 유효숫자가 딱 정해져 있다는 점 때문에 아주 큰 수의 제곱근을 구하는 데도 알맞지 않다. 아주 작은 수나 큰 수의 제곱근을 구할 때 good-enough?가 올바로 답을 내지 못하는 보기를 들어 이런 문제를 설명해 보라. 그리고 제곱근 프로시저를 고쳐 보자.

문제로 부터 얻은 것

제 생각에 가장 좋아보이는 goodenough?의 개선 방법은 $(guess)^2$과 x의 비율이 1에 가까운 지점을 기준으로 판단하는 방법입니다.

문제풀이

뉴턴법이 무엇인지는 교재의 1.1.7절을 통해 충분히 이해했다고 생각하겠습니다. 우선 정말 큰 수의 제곱근을 구하는 상황부터 살펴보겠습니다. 예로, 10,000,000,000,000의 제곱근을 구하는 과정을 생각해봅시다. 계산 흐름을 눈으로 보기 위해 improve 프로시저를 다음과 같이 수정하겠습니다.

(define (improve guess x)
  (display guess)
  (newline)
  (average guess (/ x guess)))

guess를 1로 상정한다면 아래와 같은 계산흐름을 따라갑니다.

3162277.6601683795라는 인간이 생각하기에 적당한 값을 구했음에도 불구하고, goodenough?의 조건에 맞지 않기 때문에 계속 같은 값을 계산하는 모습입니다. 이런 문제가 발생하는 이유는 goodenough?의 판단기준인 (< (- guess x) 0.001)가 매우 큰 수를 다룰 때에는 너무 높은 허들을 제시하기 때문입니다. 제곱근의 값이 크다면 보다 넓은 오차범위를 생각해야 하고, 제곱근의 값이 작다면 보다 좁은 오차범위를 생각하는 것이 사용자의 목적에 맞는 기준입니다.

또 반대로 매우 작은 수의 제곱근을 구하는 과정을 살펴보겠습니다. 이번에는 0.0000000000001의 제곱근을 구해보겠습니다.

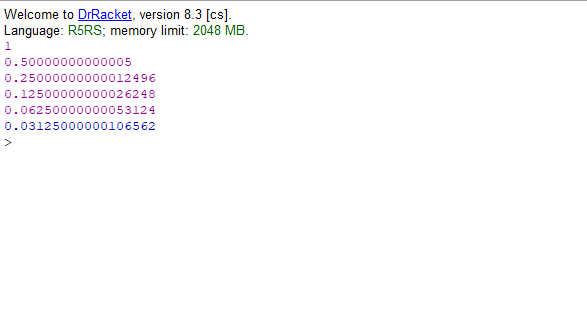
예상보다 너무 큰 숫자인 0.03125000000106562이 반환되었습니다. 참고로 이 값을 제곱하면 0.1767766953가 됩니다. 이 또한 작은 수를 다룰 때에는 좀 더 까다로운 기준을 세워야 하는데 goodenough?의 기준이 너무 쉬웠기 때문에 발생한 문제입니다.

따라서 우리가 지금부터 만들어야 하는 goodenough?는 큰 값이 들어오면 쉬운 기준을 제시하고, 작은 값이 들어오면 어려운 기준을 제시해야 합니다. 이 문제의 해결법을 찾아보던 중 가장 깔끔해 보이는 해결법을 찾았습니다. 바로 guess²와 x의 비율 즉, (/ (square guess) x)를 기준으로 생각하는 것입니다.

(define (good-enough? guess x)
  (< (abs (- (/ (square guess) x) 1)) 0.001))

위와 같이 코드를 수정하고 다시 10,000,000,000,000과 0.0000000000001을 계산해 보겠습니다.

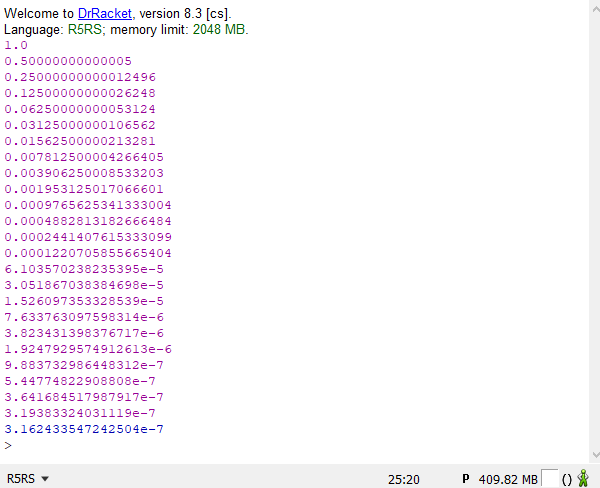
꽤나 유효한 값을 얻어내는 것을 확인할 수 있습니다.

읽어주셔서 감사합니다.