SICP 연습문제 2.19 친절한 풀이

문제

1.2.2절의 동전 바꾸기 프로그램을 살펴보자. 정해진 돈을 동전으로 바꾸는 방법이 몇 가지나 되는지 알아봤는데, 어떤 화폐로 쓸지 바꿔 끼울 수도 있도록 프로그램을 짜두면 좋다. 앞서 만든 프로그램에서는, 어떤 화폐를 쓰느냐는 first-denomination에서 결정하고, 동전 바꾸는 방법은 count-change 프로시저로 나누어 짰다(미국 동전은 다섯 가지라서 이 프로시저에는 5라는 값이 들어가 있다.). 여기에 화폐를 바꿔 끼울 수 있으려면 동전 리스트를 인자값으로 건넬 수 있어야 한다.

아울러, 두번째 인자에 어떤 동전을 쓸지 나타내는 정수값 말고, 동전 값어치의 리스트를 받을 수 있게끔 cc 프로시저를 다시 정의하려 한다. 이때, 어느나라 화폐인지에 따라 동전 리스트를 정의하면 다음과 같다.

(define us-coins (list 50 25 10 5 1))

(define uk-coins (list 100 50 20 10 5 2 1 0.5))

이렇게 고쳤을 때, cc 프로시저의 결과는 다음과 같다.

(cc 100 us-coins)
>> 292

이런 결과가 나오도록 cc 프로시저를 좀 고쳐 써야 한다. 앞에서 만들어 본 cc 프로시저의 구조는 가만히 두고, 두 번째 인자를 고쳐 써 보면 다음과 같다.

(define (cc amount coin-values)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (no-more? coin-values)) 0)
        (else
         (+ (cc amount
                (except-first-denomination coin-values))
            (cc (- amount
                   (first-denomination coin-values))
                coin-values)))))

리스트 구조를 다루는 기본 연산으로 first-denomination, except-first-denomination, no-more? 프로시저를 정의하라… coin-values 리스트 원소들의 차례가 cc 프로시저의 결과에 영향을 주는가? 그렇다면 그 까닭은 무엇인가? 또는 그렇지 않다면 그 까닭은 무엇인가?

문제로 부터 얻은 것

list를 이용해 프로시저의 표현력을 높일 수 있습니다.
왜 nil과 직접 비교하지 않고 null?을 사용하는지 알 수 있었습니다.
프로시저의 이름만으로 프로시저의 의미를 섣불리 예측할 수 없다는 것을 실감했습니다.
no-more? 프로시저는 원소가 한개만 남았을 때가 아니라, 아무것도 남지 않았을 때에 참을 반환하는 프로시저였습니다.

문제풀이

cc 프로시저가 기억나지 않으시는 분들들은 책의 1.2.2절을 다시 읽고 와주시기 바랍니다.
문제에서 요구하는 프로시저 3가지는 다음과 같습니다.

• no-more? 동전 리스트에 더이상 동전이 없는지 확인하는 프로시저
• except-first-denomination 리스트의 첫번째 원소를 제거한 리스트를 반환하는 프로시저
• first-denomination 리스트의 첫번째 원소를 반환하는 프로시저

차례로 구현하면 다음과 같습니다.

(define (no-more? x)
  (null? x))

(define (except-first-denomination x)
  (cdr x))

(define (first-denomination x)
  (car x))

책에 있는 예시로 테스트 코드를 실행시켜 보겠습니다.

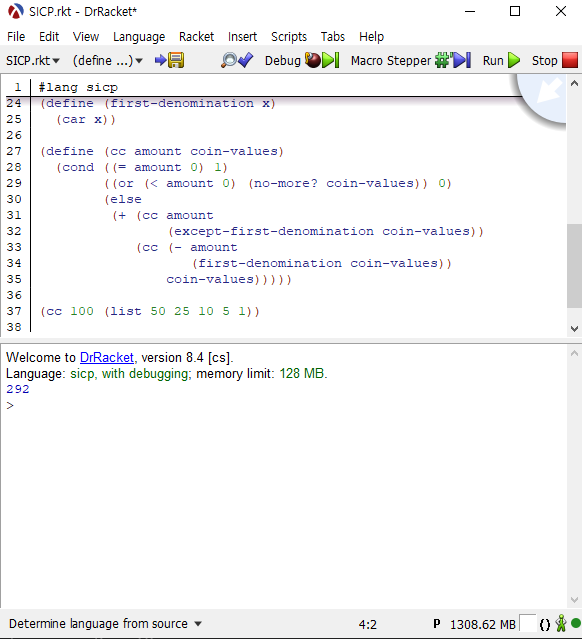
(cc 100 (list 50 25 10 5 1))
>>> 292

처음 이 문제를 풀었을 때에는 no-more?를 구현할 때 다음과 같은 코드를 사용했습니다.

(define (no-more? x)
  (= (cdr x) nil))

위의 코드가 틀린 이유는 '='는 숫자끼리만 비교가 가능하기 때문입니다.
(list 1 2 3)과 nil은 비교가 불가능합니다.

또 이렇게도 구현해 보았습니다.

(define (no-more? x)
  (= (length (cdr x)) 0))

마지막 원소가 남았을 때에 참을 반환하는 프로시저로 생각하고 있었던 것입니다.
하지만 프로시저를 다시 찬찬히 읽어보았더니 원소가 아무것도 남지 않았을 때에 참을 반환하는 프로시저였습니다.

프로시저의 이름만으로 의미를 완벽하게 추측할 수 없다는 클린코드 법칙을 실감했습니다.

읽어주셔서 감사합니다.