SICP 연습문제 2.3 친절한 풀이

문제

연습문제 2.2에서 만든 프로시저를 써서 평면에 네모꼴을 나타내는 데이터를 표현해 보자. 짜맞추개와 고르개를 써서 네모꼴의 둘레와 넓이를 구하는 프로시저를 정의하라. 이번에는 네모꼴의 표현 방법을 바꾸자. 표현 방법을 바꾸어도 둘레와 넓이 구하는 프로시저는 그대로 알맞은 요약의 경계를 갖춘 시스템을 설계할 수 있는가?

문제로 부터 얻은 것

본문의 글만 읽었을 때에는 짜맞추개와 고르개가 무엇인지 잘 몰랐습니다.
이 문제를 풀면서 짜맞추개와 고르개의 개념을 확실히 알 수 있었습니다.
또 cons를 다중으로 이용해서 짜맞추개의 요소들을 저장할 수 있다는 것을 알았습니다.

문제풀이

문제의 번역에 문제가 있습니다.
원문에는 네모꼴이 아니라 rectangle(직사각형)입니다.

1. 문제 풀이에 필요한 기본 프로시저들

(define (make-point x y)
  (cons x y))

(define (x-point p)
  (car p))

(define (y-point p)
  (cdr p))

(define (make-segment p1 p2)
  (cons p1 p2))

(define (start-segment seg)
  (car seg))

(define (end-segment seg)
  (cdr seg))

점과 점 사이의 거리를 구하는 프로시저입니다.

(define (distance-between-points p1 p2)
  (define x-diff (- (x-point p1) (x-point p2)))
  (define y-diff (- (y-point p1) (y-point p2)))
  (sqrt (+ (square x-diff) (square y-diff))))

2. 첫번째 짜맞추개와 고르개

직사각형을 어떻게 표현해야 하는 지를 오래 고민했습니다.

처음에는 모서리의 점 두개를 기준으로 직사각형을 표현하는 것을 생각했지만,
같은 모서리를 가진 직사각형은 무수히 많습니다.

그 다음으로는 점 네개를 기준으로 직사각형을 표현하는 것을 생각했지만,
점 네개는 필요 이상으로 많은 인자입니다.

결국 인터넷에서 해답을 찾았습니다.
가장 y좌표가 낮은 점인 기원점, 직사각형의 폭, 높이, 폭과 기원점이 이루는 기울기를 이용하면 깔끔하게 직사각형을 표현할 수 있습니다.
이 아이디어를 가지고 만든 짜맞추개^constructor는 다음과 같습니다.

(make-rect origin angle width height)

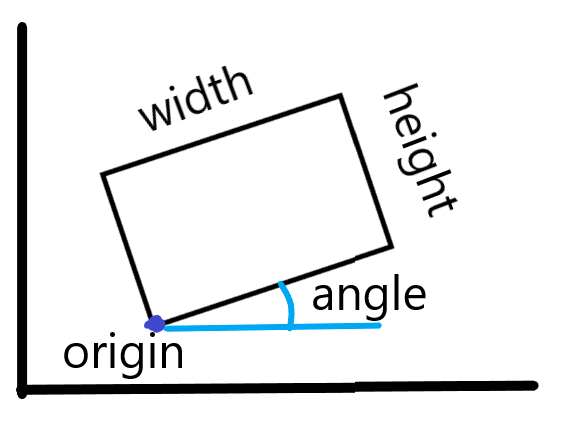
첫번째 짜맞추개와 고르개를 표현하면 다음과 같습니다.

;constructor
(define (make-rect origin angle width height)
  (cons (cons origin angle) (cons width height)))

;selector
(define (origin-rect rect) (car (car rect)))
(define (angle-rect rect) (cdr (car rect)))
(define (width-rect rect) (car (cdr rect)))
(define (height-rect rect) (cdr (cdr rect)))

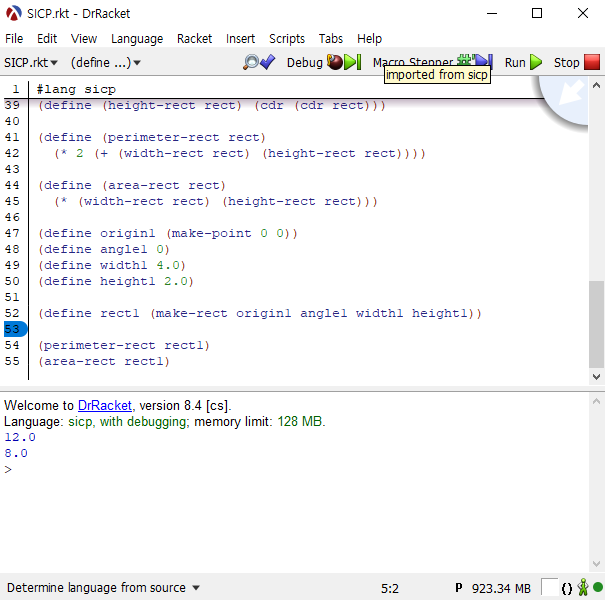
위의 짜맞추개와 고르개를 이용해 둘레와 넓이를 구하는 프로시저는 다음과 같습니다.

(define (perimeter-rect rect)
  (* 2 (+ (width-rect rect) (height-rect rect))))

(define (area-rect rect)
  (* (width-rect rect) (height-rect rect)))

시험을 위해 아래의 코드를 실행시켜 보겠습니다. 프로시저가 정상동작한다면, 둘레와 넓이를 12와 8로 계산해야 합니다.

(define origin1 (make-point 0 0))
(define angle1 0)
(define width1 4.0)
(define height1 2.0)

(define rect1 (make-rect origin1 angle1 width1 height1))

(perimeter-rect rect1)
(area-rect rect1)

3. 두번째 짜맞추개와 고르개

이번에는 세개의 점을 인자로 받아서 직사각형을 표현해 보겠습니다.

(make-rect p1 p2 p3)

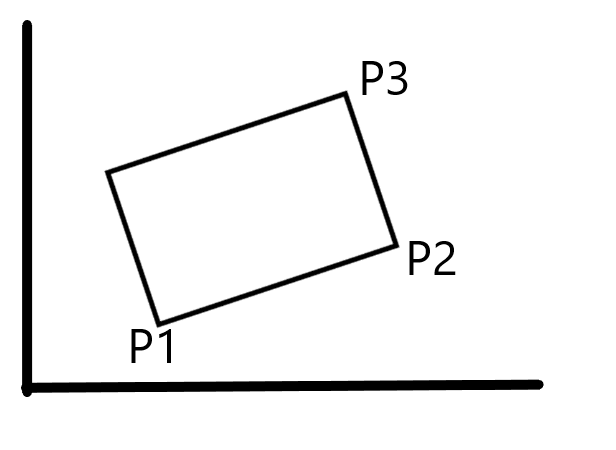
;constructor
(define (make-rect p1 p2 p3)
  (cons (cons p1 p2) p3))

;selector
(define (p1-rect rect) (car (car rect)))
(define (p2-rect rect) (cdr (car rect)))
(define (p3-rect rect) (cdr rect))

위의 짜맞추개와 고르개를 이용해 둘레와 넓이를 구하는 프로시저는 다음과 같습니다. 아래의 코드에서 주목할 점은, 실제로 둘레를 구하는 프로시저와 넓이를 구하는 프로시저는 하나도 바뀌지 않았다는 것입니다. 이는, 데이터를 사용하는 쪽과 구현하는 쪽 사이에 요약의 경계가 잘 형성되었다는 것을 의미합니다.

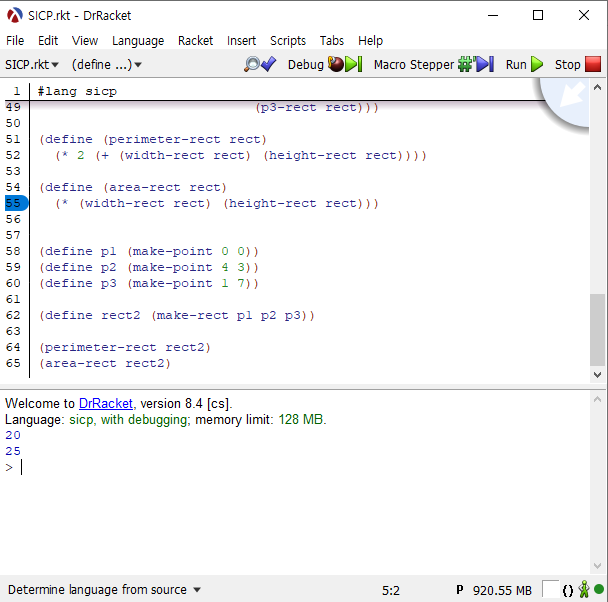
(define (width-rect rect)
  (distance-between-points (p1-rect rect)
                           (p2-rect rect)))

(define (height-rect rect)
  (distance-between-points (p2-rect rect)
                           (p3-rect rect)))

(define (perimeter-rect rect)
  (* 2 (+ (width-rect rect) (height-rect rect))))

(define (area-rect rect)
  (* (width-rect rect) (height-rect rect)))

시험을 위해 아래의 코드를 실행시켜 보겠습니다. 프로시저가 정상동작한다면, 둘레와 넓이를 20과 25로 계산해야 합니다.

(define p1 (make-point 0 0))
(define p2 (make-point 4 3))
(define p3 (make-point 1 7))

(define rect2 (make-rect p1 p2 p3))

(perimeter-rect rect2)
(area-rect rect2)

4. 두 개의 방식을 비교

우의 두가지 방식에서 눈여겨볼 점이 있습니다. 두가지 방식의 구현에서 짜맞추개와 고르개를 서로 다르게 설계했지만, 둘레와 넓이를 구하는 프로시저의 코드는 결국 동일하다는 것입니다. 두 데이터 표현형은 서로 같은 코드의 perimeter와 area-rect를 공유할 수 있습니다.

perimeter와 area-rect 프로시저의 입장에서 바라보는 width-rect와 height-rect 프로시저는, 내부가 어떻게 구현되어 있는지는 몰라도 동일한 결과를 가져다 주는 프로시저입니다. 이 프로시저들의 사이에 책에서 설명한 요약의 경계가 있는 것입니다.

본문의 글만 읽었을 때에는 짜맞추개와 고르개가 무엇인지 잘 몰랐습니다. 이 문제를 풀면서 짜맞추개와 고르개의 개념을 확실히 알 수 있었습니다. 또 cons를 다중으로 이용해서 짜맞추개의 요소들을 저장할 수 있다는 것을 알았습니다.

읽어주셔서 감사합니다.