SICP 연습문제 2.32 친절한 풀이

문제

같은 원소가 되풀이되지 않는 리스트로 집합을 나타낼 수 있다. 또한, 한 집합의 모든 부분 집합의 집합은 리스트의 리스트로 나타낼 수 있다. 리스트 (1 2 3)을 집합으로 보면, 모든 부분집합의 집합은 (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))이 된다. 한 집합의 모든 부분 집합의 집합을 구하는 프로시저를 아래와 같이 정의할 수 있다. 빈 곳을 채워 이 프로시저를 완성하고, 이 프로시저가 어떻게 돌아가는지 설명하라.

(define (subsets s)
  (if (null? s)
      (list nil)
      (let ((rest (subsets (cdr s))))
        (append rest (map <??> rest)))))

문제로 부터 얻은 것

부분집합을 만드는 수학적 원리를 프로시저로 구현하면서 리스트 처리의 이해도를 높일 수 있었습니다.

문제풀이

(list 1 2 3)의 부분집합을 만드는 원리를 설명해 보겠습니다.

1. 가장 첫번째 원소를 고릅니다.
2. 나머지 원소들로 이루어진 리스트의 부분집합을 구했다고 가정해 봅시다.
3. 전체 부분집합은, 나머지 원소들의 부분집합에 선택한 첫번째 원소를 포함한 집합과 포함하지 않은 집합의 합으로 구할 수 있습니다.

(1 2 3)을 예로들자면, 집합 (2 3)의 모든 부분집합에 1을 포함시킨 집합과 그냥 (2 3)의 모든 부분집합을 더하면 전체 부분집합을 알 수 있다는 것입니다. 이는 1을 포함한 부분집합과 1을 포함하지 않은 부분집합을 더한다는 의미로도 해석할 수 있습니다.

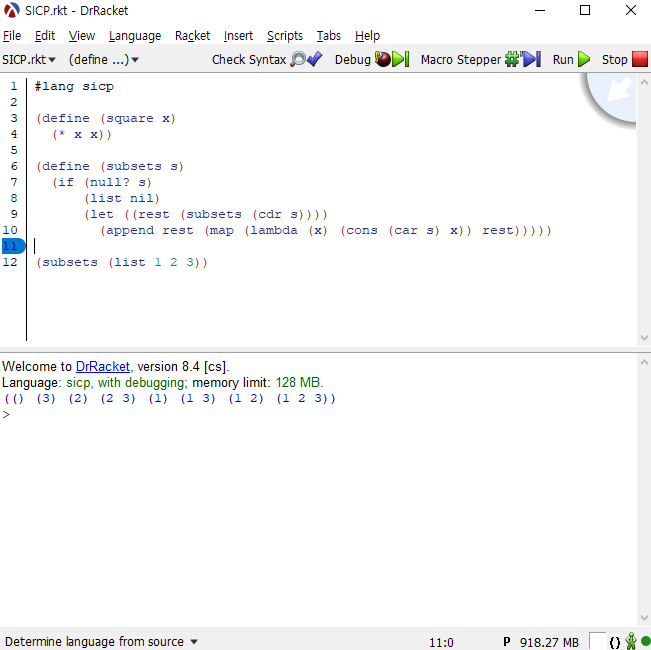
(define (subsets s)
  (if (null? s)
      (list nil)
      (let ((rest (subsets (cdr s))))
        (append rest (map (lambda (x) (cons (car s) x)) rest)))))

읽어주셔서 감사합니다.