SICP 연습문제 2.34 친절한 풀이

문제

아래와 같이 정의된 x의 다항식 값 계산 과정을 accumulate로 나타내 보자.

$a_nx^n+a_{n-1}x^{n-1}+⋯+a_1x +a_0$

위 다항식은 호너의 규칙^{Honer’s rule}이라는 알고리즘을 서서 다음 방식으로 계산할 수 있다.

$(⋯(a_nx+a_{n-1})x+⋯+a_1)x +a_0$

다시 말하면, $a_n$에 $x$를 곱한 다음 $a_{n-1}$을 더하고, 그 값에 다시 $x$를 곱하는 방식으로 $a_0$에 이를 때까지 계산을 이어간다. 아래에서 빈 곳을 매워, 호너의 규칙에 따라 다항식을 구하는 프로시저의 정의를 마무리하라. 이때, 다항식의 계수들은 $a_0$에서 $a_n$까지 차례열 속에 들어 있다고 하자.

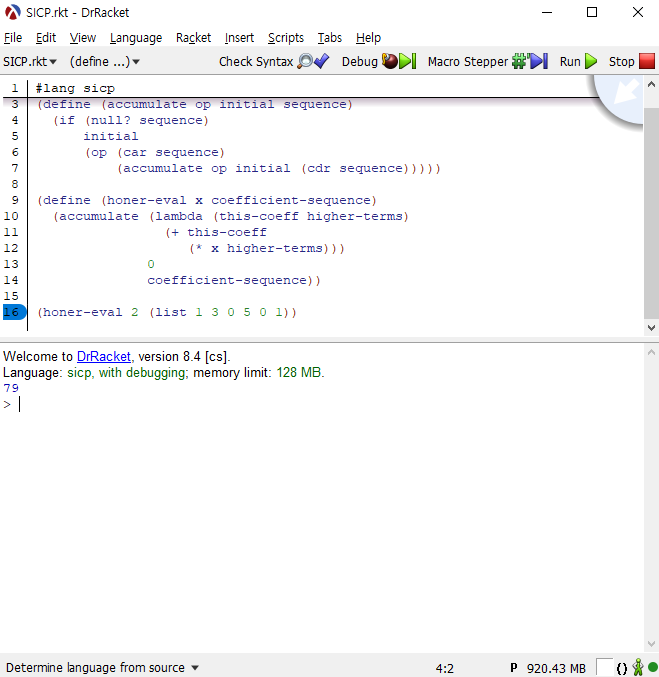
(define (honer-eval x coefficient-sequence)
  (accumulate (lambda (this-coeff higher-terms) <??>)
              0
              coefficient-sequence))

보기를 들어, $x=2$일 때 $1+3x+5x^3+x^5$의 값을 계산하는 식은 다음과 같다.

(honer-eval 2 (list 1 3 0 5 0 1))

문제로 부터 얻은 것

차례열 연산의 핵심 부품인 accumulate 프로시저의 이해도를 높일 수 있었습니다.

문제풀이

문제 풀이에 사용할 accumulate 프로시저는 다음과 같습니다.

(define (accumulate op initial sequence)
  (if (null? sequence)
      initial
      (op (car sequence)
          (accumulate op initial (cdr sequence)))))

문제의 (honer-eval x coefficient-sequence) 프로시저를 다시 해석해 보면, coefficient-sequence에 들어가는 리스트의 원소들은 차례로 $x^0$의 계수, $x^1$의 계수,$x^2$의 계수,$⋯$를 의미하는 것입니다. 이제 아래의 식을 람다식으로 표현하는 일만 남았습니다.

$(⋯(a_nx+a_{n-1})x+⋯+a_1)x +a_0$

(현재의 단계의 계수) + x*(다음으로 처리할 계수들)을 반복하는 것으로 구현할 수 있습니다.

(define (honer-eval x coefficient-sequence)
  (accumulate (lambda (this-coeff higher-terms)
                (+ this-coeff
                   (* x higher-terms)))
              0
              coefficient-sequence))

$1+3x+5x^3+x^5 \ \ ,x=2$

$= 1+6+40+32=79$

읽어주셔서 감사합니다.