SICP 연습문제 2.37 친절한 풀이

문제

벡터 $v=(v_i)$는 수열^{sequence of numbers}로 나타내고, 행렬 $m=(m_{ij})$은 다시 벡터 (행렬의 행)들의 차례열로 나타내기로 하자. 이를테면, 아래 행렬은 차례열 ((1 2 3 4) (4 5 6 6) (6 7 8 9))로 나타낸다.

$\begin{bmatrix} 1&2&3&4\\ 4&5&6&6\\ 6&7&8&9 \end{bmatrix}$

이런 표현 방식을 바탕으로 하면, 다음과 같은 (행렬 대수 책에 흔히 나오는) 행렬과 벡터 연산들을 차례열 연산으로 간결하게 나타낼 수 있다.

$(dot-product \ \ v \ \ w)$

$Σ_iv_iw_i$

$(matrix-*-vector \ \ m \ \ v)$

$when \ \ t_i=Σ_jm_{ij}v_j, \ \ vector \ \ t$

$(matrix-*-matrix \ \ m \ \ n)$

$when \ \ P_{ij}=Σ_km_{ik}n_{kj}, \ \ matrix \ \ P$

$(transepose \ \ m)$

$n_{ij}=m_{ji} \ \ matrix \ \ n$

행렬을 내적^{dot product}하는 연산은 다음처럼 정의할 수 있다.
여기서 사용하는 map은 스킴에 내장된 기본 프로시저입니다. 기존까지 사용하던 map과는 다르게 같은 길이의 리스트를 여러개 인자로 받을 수 있습니다. 자세한 설명은 한글번역 책의 136p 하단의 각주 12)에 있습니다.

(define (dot-product v w)
  (accumulate + 0 (map * v w)))

아래 식에서 빈 곳을 채워 행렬 연산 프로시저의 정의를 모두 마무리하라.
(accumulate-n은 연습문제 2.36에서 정의했다.)

(define (matrix-*-vector m v)
  (map <??> m))
  
(define (transpose mat)
  (accumulate-n <??> <??> mat))
  
(define (matrix-*-matrix m n)
  (let ((cols (transpose n)))
    (map <??> m)))

문제로 부터 얻은 것

익숙하지 않은 행렬 연산과 익숙하지 않은 차례열 처리로 뇌가 말랑말랑해지는 시간이었습니다.

문제풀이

저는 고등교육과정에서 행렬이 빠진 세대입니다. 그래서 그런지 행렬연산 문제가 나올 때마다 구글링으로 행렬곱을 찾아봐야 합니다.

a. matrix와 vector의 내적

(define (matrix-*-vector m v)
  (map <??> m))

map은 행렬의 열을 하나씩 처리할 수 있도록 도와줍니다. 즉 물음표 안에는 각 열을 벡터와 내적해주는 프로시저가 들어가야 합니다.

(define (matrix-*-vector m v)
  (map (lambda (x) (dot-product x v)) m))

b. matrix의 전치행렬

(define (transpose mat)
  (accumulate-n <??> <??> mat))

전치 행렬은 accmumulate-n을 이용하면 어렵게 생각하지 않아도 구할 수 있습니다.

(define (transpose mat)
  (accumulate-n cons nil mat))

c. matrix와 matrix의 행렬곱

(define (matrix-*-matrix m n)
  (let ((cols (transpose n)))
    (map <??> m)))

행렬의 곱에 익숙하지 않은 저는, 구현하기도 어려웠고 설명하기도 어려웠습니다. 제 논리의 흐름을 보여드리겠습니다.

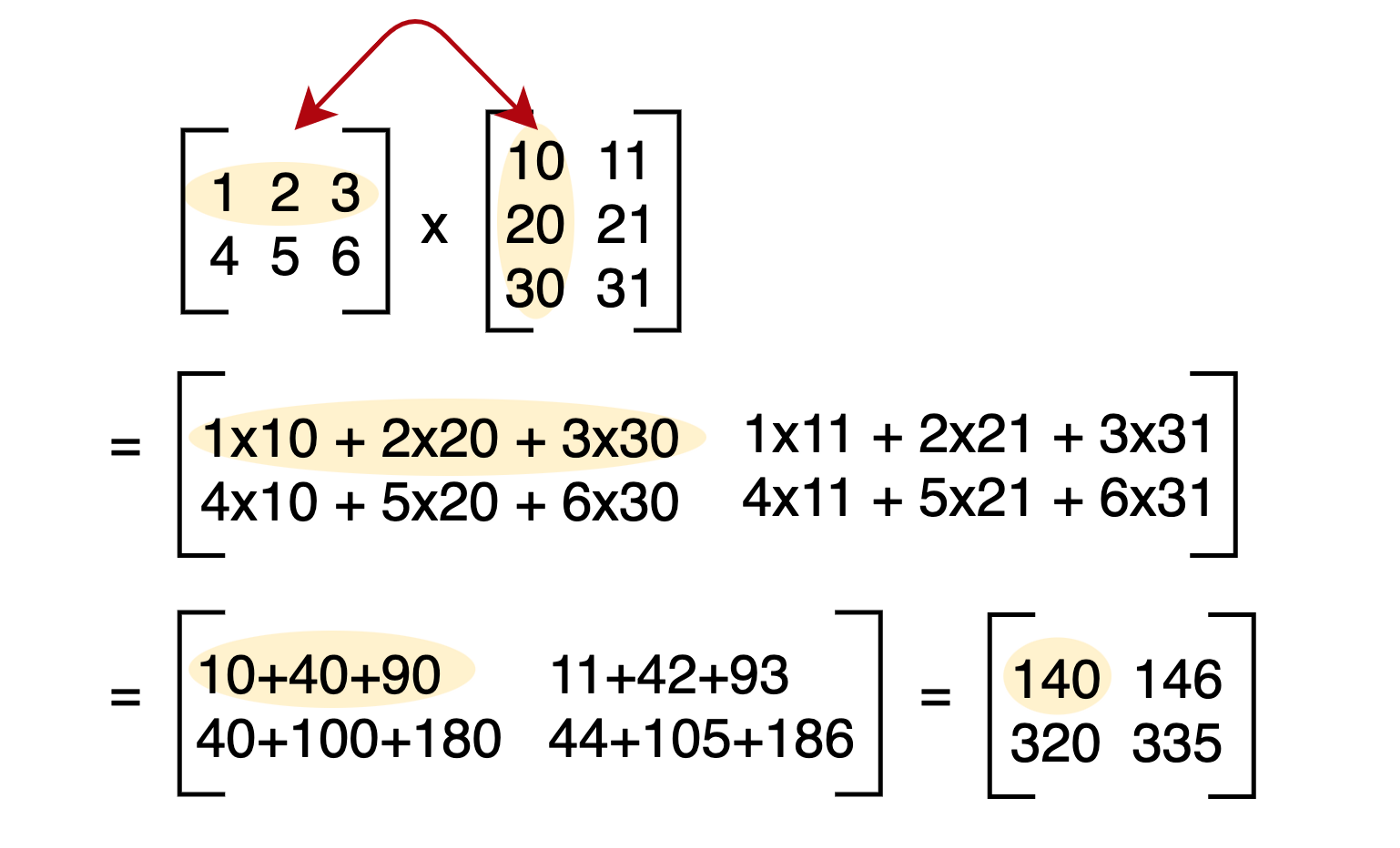
1. (map <??> m)에서 물음표 프로시저가 하는 일은, m의 row마다 cols를 이용한 어떤 처리를 해주는 일이다.
2. 그 처리는 cols의 row들 하나하나와 m으로부터 받은 row를 내적한 값을 cols의 길이만큼의 벡터로 반환하는 것이다. 이것은 행렬과 벡터의 곱이다.

위의 아이디어를 코드로 구현하면 아래와 같습니다.

(define (matrix-*-matrix m n)
  (let ((cols (transpose n)))
    (map (lambda (row-from-m)
           (matrix-*-vector cols row-from-m))
         m)))

d. 테스트 코드로 확인

matrix-*-matrix 프로시저에는 이 문제에서 만든 모든 프로시저가 들어가 있으므로 아래의 식이 제대로 동작하면 모든 프로시저가 정상적으로 동작하는 것입니다.

(define m1 (list (list 1 2 3) (list 4 5 6)))

(define m2 (list (list 10 11) (list 20 21) (list 30 31)))

(matrix-*-matrix m1 m2)

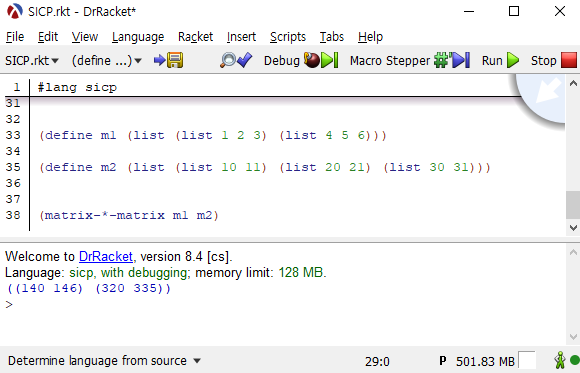
읽어주셔서 감사합니다.