SICP 연습문제 2.41 친절한 풀이

문제

어떤 정수 n보다 작거나 n과 같은, 서로 다른 양의 정수 i,j,k가 있다고 할 때, 그 합이 어떤 정수 s가 된다고 하자. 그와 같은 세 정수의 트리플을 차례대로 뽑아내는 프로시저를 짜라.

문제로 부터 얻은 것

flatmap을 사용해야 하는 곳과 map을 사용해야 하는 곳을 구별할 수 있게 되었습니다.
map은 시퀀스의 원소 각각에 대해 산출값이 하나씩만 있는 문제에 쓰입니다.
반면 flatmap은 시퀀스의 원소 각각에 대해 산출값이 여러개인 문제에 쓰입니다.

문제풀이

이전 문제인 연습문제 2.40에서 영감을 얻어서, n보다 작은 수로 이루어진 트리플들의 차례열을 먼저 만든 다음 filter를 사용하는 방향으로 풀이의 방향을 잡았습니다.

a. n보다 작은 수의 트리플

처음 이 프로시저를 구상할 때에는 flatmap을 세 번 사용했습니다. 그리고 당연히 그 방법은 틀렸습니다. flatmap을 두번 사용한 뒤에는 map을 사용해야 합니다. 첫번째 flatmap의 람다함수가 하는 역할은, i하나를 받아서 i가 포함된 트리플들을 반환하는 것입니다. 두번째 flatmap의 람다함수의 역할은 j 하나를 받아서 선택된 i와 선택된 j가 포함된 트리플들을 반환하는 것입니다. 그렇다면 여기서 이미 i와 j값이 정해져 있을때, 트리플을 반환하는 방법은 flatmap이 아니라 map을 사용해 1~n까지의 수만큼의 트리플을 반환하는 것입니다. 그러므로 프로시저는 아래와 같습니다.

(define (unique-triples n)
  (let ((range (enumerate-interval 1 n)))
    (flatmap (lambda (i)
             (flatmap (lambda (j)
                        (map (lambda (k) (list i j k))
                             range))
                      range))
           range)))

b. 필터로 구현한 프로시저

프로시저에 사용될 필터를 구현하는 것은 어렵지 않습니다. 차례열을 인자로 받아서 그 합이 s와 같은지 판별하는 프로시저를 만들면 됩니다. 이 프로시저는 필터 프로시저에 들어가야 하므로 람다식의 형태로 만듭니다.

(define (is-sum-to s)
  (lambda (seq) (= s (accumulate + 0 seq))))

완성된 프로시저입니다.

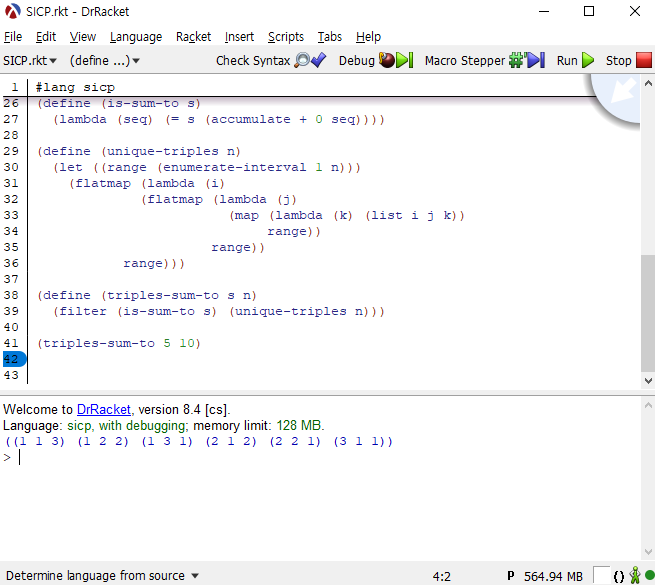
(define (triples-sum-to s n)
  (filter (is-sum-to s) (unique-triples n)))

읽어주셔서 감사합니다.