SICP 연습문제 2.56 친절한 풀이

문제

앞서 본 것들이 타입이 다른 식을 처리할 수 있게끔, 미분 프로그램의 쓰임새를 어떻게 늘리는지 밝혀라. 보기를 들어, 가음 규칙을 실현할 수 있도록 deriv 프로그램에 새로운 마디를 하나 더하고 그에 알맞은 exponentiation?, base, exponent, make-exponentiation을 정의하라.

$\frac{d(u^n)}{dx} = nu^{n-1}\frac{du}{dx}$

(지수 연산을 나타내는 데는 **같은 글자를 쓸 수 있겠다.) 아울러 ‘무엇의 0승은 1’, '무엇의 1승은 바로 그 무엇’이라는 규칙에 따라, 줄어든 식이 나올 수 있게끔 하라.

문제로 부터 얻은 것

대수식을 프로시저로 표현하는 법을 연습할 수 있었습니다.

문제풀이

a. 기본 프로시저

책에 적혀있는 문제를 푸는데 필요한 프로시저들입니다.

(define (variable? x) (symbol? x)) 

(define (same-variable? v1 v2) 
 (and (variable? v1) (variable? v2) (eq? v1 v2))) 

(define (make-sum a1 a2) 
 (cond ((=number? a1 0) a2) 
       ((=number? a2 0) a1) 
       ((and (number? a1) (number? a2)) (+ a1 a2)) 
       (else (list '+ a1 a2)))) 

(define (make-product m1 m2) 
 (cond ((or (=number? m1 0) (=number? m2 0)) 0) 
       ((=number? m1 1) m2) 
       ((=number? m2 1) m1) 
       ((and (number? m1) (number? m2)) (* m1 m2)) 
       (else (list '* m1 m2)))) 
 
(define (=number? exp num) 
 (and (number? exp) (= exp num))) 

(define (sum? x) 
 (and (pair? x) (eq? (car x) '+))) 

(define (addend s) (cadr s)) 

(define (augend s) (caddr s)) 

(define (product? x) 
 (and (pair? x) (eq? (car x) '*))) 

(define (multiplier p) (cadr p)) 

(define (multiplicand p) (caddr p)) 

b. deriv 수정

우선 지수 연산의 규칙들을 프로시저로 표현해 보겠습니다.

$if \ \ b \neq 0$

$\frac{d(b^n)}{dx} = nb^{n-1}\frac{db}{dx}$

(make-product n
              (make-exponentiation b (make-sum n -1))
              (deriv b x))

그런데, make-product는 인자를 두개만 받으므로

(make-product n
              (make-product (make-exponentiation b (make-sum n -1))
                            (deriv b x))))) 

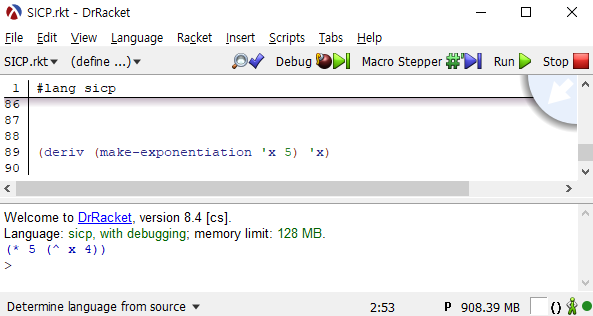
위의 식을 바탕으로 책에 나와있는 deriv 프로시저에 지수연산과 관련된 절을 추가하겠습니다.

(define (deriv exp var)   
  (cond ((number? exp) 0) 
        ((variable? exp)
         (if (same-variable? exp var) 1 0)) 
        ((sum? exp)
         (make-sum (deriv (addend exp) var)   
                   (deriv (augend exp) var))) 
        ((product? exp)
         (make-sum
          (make-product (multiplier exp)
                        (deriv (multiplicand exp) var))
          (make-product (deriv (multiplier exp) var)
                        (multiplicand exp)))) 
        ((exponentiation? exp) 
         (let ((b (base exp)) (n (exponent exp))) 
           (make-product n
                         (make-product (make-exponentiation b (make-sum n -1))
                                       (deriv b var))))) 
        (else "unknown expression type")))

c. 대수식 표현

그리고 데이터 타입을 표현하는 대수식들을 구현하겠습니다. 거듭제곱의 연산기호로는 "^"를 사용하겠습니다.

(define (exponentiation? exp)
  (and (pair? exp) (eq? (car exp) '^)))

(define (base exp) (cadr exp))

(define (exponent exp) (caddr exp))

(define (make-exponentiation b n)
  (cond ((=number? b 0) 0)
        ((=number? b 1) 1)
        ((=number? n 0) 1)
        ((=number? n 1) b)
        ((and (number? b) (number? n)) (pow b n))
        (else (list '^ b n))))

앞 절의 내용을 잘 이해했다면 구현하는 데에 크게 무리는 없습니다.

읽어주셔서 감사합니다.