SICP 연습문제 2.57 친절한 풀이

문제

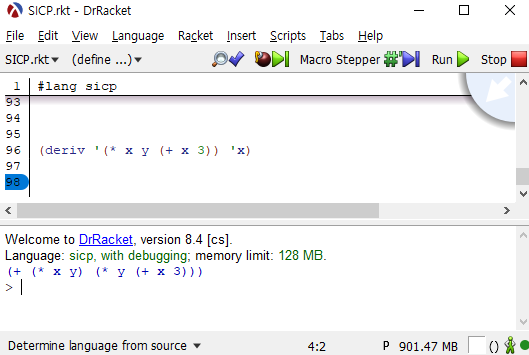
미분 프로그램의 쓰임새를 늘려서 (둘보다 많은) 여러 마디로 이루어진 덧셈 식과 곱셈 식을 처리할 수 있도록 하자. 그리 되면, 위에서 맨 끝에 든 보기를 다음과 같이 표현할 수 있다.

(deriv '(* x y (+ x 3)) 'x)

이 문제를 풀 때, deriv 프로그램은 손대지 말고 덧셈 식과 곱셈 식을 표현하는 방법만 바꾸도록 하라. 예컨대, 덧셈 식에서 augend는 첫 번째 마디를 가리키고, addend는 나머지 모든 마디의 덧셈 식을 가리키게 된다.

문제로 부터 얻은 것

리스트의 마지막 원소까지 cdr을 해도 마지막 원소와 nil을 인자로 가지는 리스트가 반환되므로, pair?를 통과한다는 것을 알게 되었습니다.
deriv 프로시저를 일절 수정하지 않고도 멋진 일을 할 수 있다는 것을 알았습니다.

문제풀이

기존의 deriv 프로시저는 '(* x y z)같은 인자를 미분하지 못했습니다. 이는 make-multiplication 프로시저가 인자를 두개밖에 받지 못하기 때문에 deriv를 구현할 때도 세개 이상의 인자를 고려하지 않았기 때문입니다. 덧셈과 곱셈의 이런 문제는 augend와 multiplicand를 수정함으로서 해결할 수 있습니다. 간단히 (+ x y z)의 augend를 (+ y z)로 반환하면 되는 것입니다. 구현한 프로시저는 아래와 같습니다.
이미 아시겠지만, cdddr은 cdr을 세번 겹쳐 쓴 것이고, caddr은 cdr을 두번 겹쳐쓴 뒤, car을 사용한 것입니다.

(define (augend s)
  (if (pair? (cdddr s))
      (make-sum (caddr s)
                (augend (cdr s)))
      (caddr s)))

(define (multiplicand p)
  (if (pair? (cdddr p))
      (make-product (caddr p)
                    (multiplicand (cdr p)))
      (caddr p))) 

위의 프로시저에서 왜 (pair? (cddr s))가 아닌 (pair? (cdddr s))가 되는지 궁금하신 분들도 계실 겁니다. '(+ x y)의 식을 예로 들겠습니다. '(+ x y)에 cddr을 적용하면, y를 반환하는 것이 아닌, (y)를 반환합니다. 다른 표현방식을 빌리자면, (cons y nil)을 반환하는 것입니다. pair?는 이런 데이터도 참으로 반환하기 때문에 cdddr을 적용해서 nil을 반환하도록 하는 것입니다.

(deriv '(* x y (+ x 3)) 'x)

읽어주셔서 감사합니다.