SICP 연습문제 2.61 친절한 풀이

문제

차례 매긴 리스트 표현에 따라 adjoin-set을 구현하라. element-of-set?와 비슷하게, 차례 없는 표현 방식과 견주어 그 계산 단계가 평균하여 반으로 줄어들도록 프로시저를 짜는데, 차례 매김 표현 방식의 좋은 점이 어떻게 도움이 되는지 보여라.

문제로 부터 얻은 것

정렬된 인자를 처리할때, 프로시저를 짜기 편할 뿐더러 실행 시간도 줄일 수 있음을 알 수 있었습니다.

문제풀이

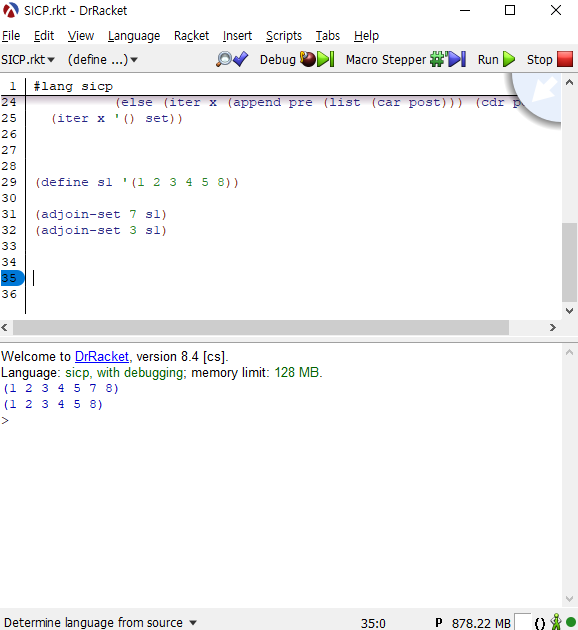
집합의 원소가 정렬되어 있으므로, 책에서 설명한 element-of-set?과 마찬가지로 순차적으로 검색하면서 x보다 큰 원소가 있는 지점을 찾으면 됩니다. 이때 x보다 작은 값들과 x보다 큰 값들을 pre와 post에 저장하고 iter를 돌면 쉽게 구현할 수 있습니다.

(define (adjoin-set x set)
  (define (iter x pre post)
    (cond ((null? post) (append (append pre (list x)) post))
          ((< x (car post)) (append (append pre (list x)) post))
          ((= x (car post)) set)
          (else (iter x (append pre (list (car post))) (cdr post)))))
  (iter x '() set))

이 프로시저는 set을 순차적으로 검색하므로 가장 큰 값을 원소로 넣는다면, 프로시저는 n시간이 걸릴 것입니다. 반대로 가장 작은 값을 원소로 넣는다면 1만큼 시간이 걸릴것입니다. 즉 평균적으로 n/2의 시간이 걸린다고 할 수 있으므로, 이 프로시저의 시간 복잡도는 $Θ(n)$입니다. 기존의 프로시저도 시간복잡도 상으로는 같은 $Θ(n)$이지만, 항상 n만큼의 시간이 걸립니다. 반면 이번에 만든 프로시저는 평균적으로 n/2시간이 걸리므로 이번에 만든 프로시저가 좀더 성능이 좋다고 할 수 있습니다.

(define s1 '(1 2 3 4 5 8))

(adjoin-set 7 s1)
(adjoin-set 3 s1)

읽어주셔서 감사합니다.