SICP 연습문제 2.63 친절한 풀이

문제

아래 두 프로시저는 두 갈래 나무를 리스트로 바꾼다.

(define (tree->list-1 tree)
  (if (null? tree)
      '()
    (append (tree->list-1 (left-branch tree))
            (cons (entry tree)
                    (tree->list-1 (right-branch tree))))))

(define (tree->list-2 tree)
  (define (copy-to-list tree result-list)
    (if (null? tree)
        result-list
        (copy-to-list (left-branch tree)
                      (cons (entry tree)
                            (copy-to-list (right-branch tree)
                                          result-list)))))
  (copy-to-list tree '()))  

a. 두 프로시저는 어떤 나무를 집어 넣어도 같은 결과를 내는가? 아니라면, 그 결과가 어떻게 다른가? 그림 2.16의 나무를 집어 넣을 때, 두 프로시저는 어떤 리스트를 내놓는가?

b. 원소 수가 n인 균형 잡힌 나무를 리스트로 바꾼다고 할 때, 위 프로시저들이 밟아야 할 계산 단계는 똑같은 자람 차수를 보이는가? 그게 아니라면, 계산 단계가 더 느리게 자라나는 쪽은 어느 쪽인가?

문제로 부터 얻은 것

append를 cons로 바꾸는 것 만으로 시간복잡도가 크게 달라지는 것을 알았습니다.
시간복잡도를 구할 때는 노트에 써서 하나 하나 계산하는 것이 가장 좋은 방법이라는 것을 알았습니다.

문제풀이

(define (entry tree) (car tree))
(define (left-branch tree) (cadr tree))
(define (right-branch tree) (caddr tree))

a. 두 프로시저의 결과

책의 그림 2.16에 있는 트리들을 코드로 구현하면 아래와 같습니다. make-tree를 사용할 수도 있지만, 지금은 간단하게 따옴표 표기로 표현했습니다. 여기서 책을 꼼꼼히 잘 읽었다면 마지막 이파리의 원소를 (n () ())꼴로 표기하는 것을 눈치챌 수 있을 것입니다. 저는 별로 꼼꼼히 읽지 못해서 그만 n으로 표기하는 실수를 범했었습니다. 여러분은 그러지 않으셨기를 바랍니다.

(define t1 '(7 (3 (1 () ())
                  (5 () ()))
               (9 ()
                  (11 () ()))))

(define t2 '(3 (1 () ())
               (7 (5 () ())
                  (9 ()
                     (11 () ())))))

(define t3 '(5 (3 (1 () ())
                  ())
               (9 (7 () ())
                  (11 () ()))))

(tree->list-1 t1)
(tree->list-2 t1)

(tree->list-1 t2)
(tree->list-2 t2)

(tree->list-1 t3)
(tree->list-2 t3)

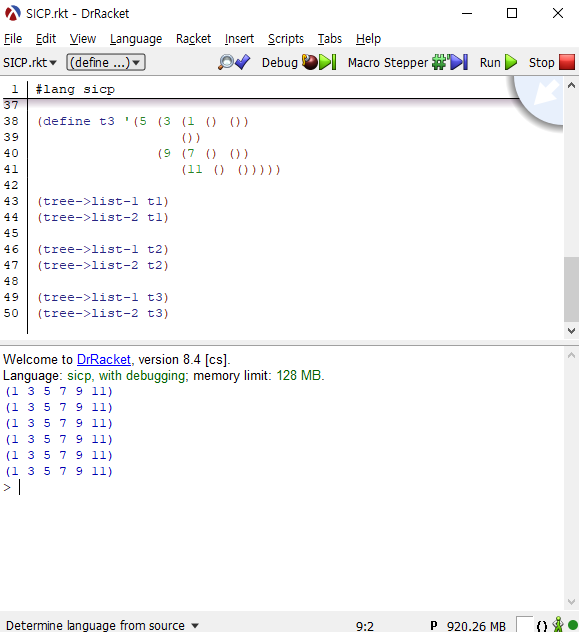
모든 트리가 동일한 결과를 보이는 모습입니다.

b. 균형잡힌 트리

우선 tree->list-1부터 살펴보겠습니다. 이 프로시저는 각 엔트리에 대해서 (왼쪽 가지 리스트, 엔트리, 오른쪽 가지 리스트) 순으로 리스트를 엮어 반환하는 프로시저입니다. 여기서 발견할 수 있는 점은, 트리에 있는 모든 원소에 이 프로시저가 한번씩은 적용된다는 것입니다. 심지어 노드의 끝마디에 붙어있는 '()에까지 프로시저를 적용한다는 것을 알 수 있습니다. 그러므로 이 프로시저의 총 실행 횟수는 전체 원소의 갯수 + 전체 '()의 갯수입니다. 그런데, 한 트리의 원소의 갯수가 같다면 '()의 갯수도 같다는 것을 쉽게 알 수 있습니다. 어떤 트리에서 하나의 원소가 자리를 옮기면, 그 자리에 nil이 하나 생기고, 원래 nil이 있던 자리에 새로운 원소가 오므로 전체 nil의 개수는 같습니다.

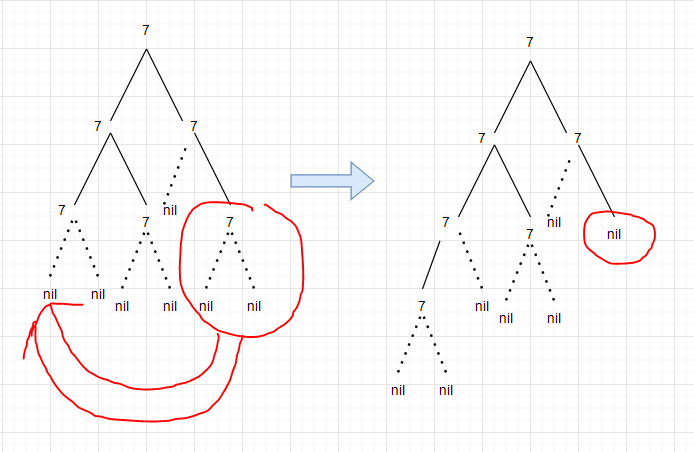
tree->list-2도 마찬가지로 모든 엔트리와 nil에 적용되는 프로시저이므로 실행 횟수는 동일합니다. 이를 확실히 알아보기 위해서 두 프로시저를 다음과 같이 추가해서, 프로시저가 실행될 때마다 1을 출력하도록 해보겠습니다.

(define (tree->list-1 tree)
  (display "1")
  (if (null? tree)
      '()
    (append (tree->list-1 (left-branch tree))
            (cons (entry tree)
                    (tree->list-1 (right-branch tree))))))

(define (tree->list-2 tree)
  (define (copy-to-list tree result-list)
    (display "1")
    (if (null? tree)
        result-list
        (copy-to-list (left-branch tree)
                      (cons (entry tree)
                            (copy-to-list (right-branch tree)
                                          result-list)))))
  (copy-to-list tree '())) 

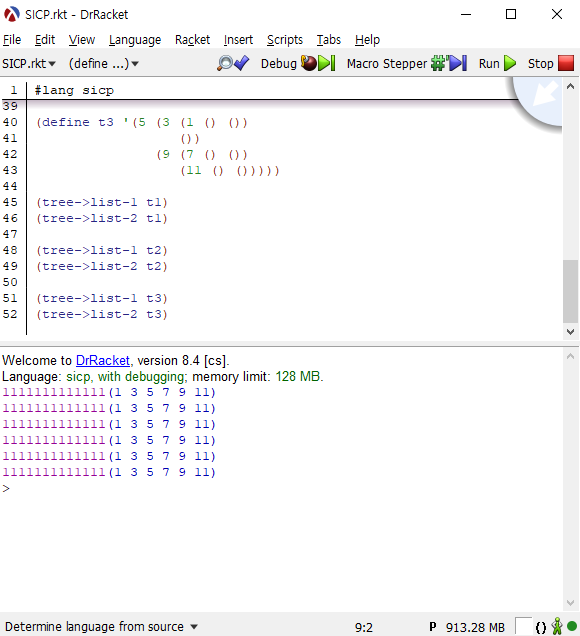
그러므로 두 프로시저의 실행 횟수는 동일합니다. 하지만, 그렇다고 해서 자람 차수가 동일한 것은 아닙니다. 1번 프로시저는 엮어내는 방식으로 append를 사용하고 있고, 2번 프로시저는 cons를 사용하고 있습니다.

append는 n이 커짐에 따라 자람 차수가 커지는 $Θ(n)$의 프로시저입니다. 그리고 여기서 n은 append의 첫번째 인자를 제외한 나머지 인자의 원소들의 갯수를 의미합니다.

$T(n)$을 프로시저를 실행하는데 필요한 시간이라고 하겠습니다.
1번 프로시저는 $T(n)=2T(n/2) + Θ(n)$을 만족한다고 볼 수 있습니다.
2번 프로시저는 $T(n)=2T(n/2) + Θ(1)$을 만족한다고 볼 수 있습니다.

아래의 그림은 1번 프로시저의 시간복잡도를 구하는 그림입니다. 각 단계에서 append 프로시저는 $Θ(n)$의 시간복잡도를 차지합니다. 그리고 단계의 크기가 $log_2 n$이므로, 이 둘을 곱하면 1번 프로시저의 시간복잡도를 알 수 있습니다.

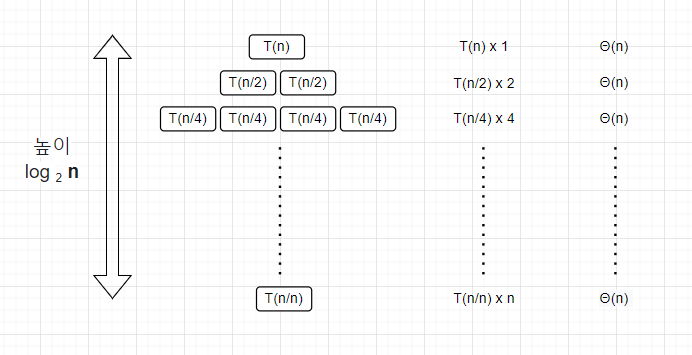
즉, 1번 프로시저는 $Θ(n)$이 $log_2 n$만큼 실행되므로 $Θ(n\log{n})$의 시간복잡도를 가집니다.

2번 프로시저는 $Θ(1)$인 cons를 사용하므로 $Θ(n)$의 시간복잡도를 가집니다.

난해한 설명 읽어주셔서 감사합니다.