SICP 연습문제 2.64 친절한 풀이

문제

다음에 나오는 프로시저 list->tree는 차례 매긴 리스트를 균형 잡힌 두 갈래 나무로 바꾼다. 도우미 프로시저^{helper procedure} partial-tree는 정수 n과, 원소 수가 적어도 n개인 리스트를 인자로 받아서, 그 리스트의 처음 n개 원소로 균형 잡힌 나무를 만든다. partial-tree는 (cons로 만든) 쌍을 결과로 내놓는데, 이 쌍의 car는 새로 만든 나무를 가리키고 그 cdr는 그 나무에서 빠진 원소들의 리스트를 가리킨다.

(define (list->tree elements)
  (car (partial-tree elements (length elements))))

(define (partial-tree elts n)
  (if (= n 0)
      (cons '() elts)
      (let ((left-size (quotient (- n 1) 2)))
        (let ((left-result (partial-tree elts left-size)))
          (let ((left-tree (car left-result))
                (non-left-elts (cdr left-result))
                (right-size (- n (+ left-size 1))))
            (let ((this-entry (car non-left-elts))
                  (right-result (partial-tree (cdr non-left-elts)
                                              right-size)))
              (let ((right-tree (car right-result))
                    (remaining-elts (cdr right-result)))
                (cons (make-tree this-entry left-tree right-tree)
                      remaining-elts))))))))

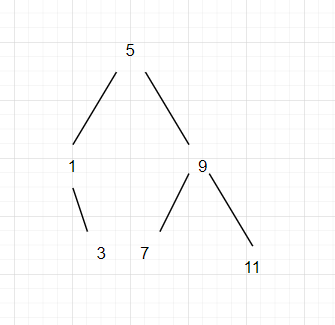
a. partial-tree 프로시저가 어떻게 돌아가는지 되도록 깔끔하고 짧은 문장으로 설명해 보라. 리스트 (1 3 5 7 9 11)를 list->tree에 인자로 넘길 때, 어떤 나무가 나오는지 그려 보라.

b. list->tree로 원소 수가 n인 리스트를 바꾸는 데 드는 계산 단계는 어떤 자람 차수를 보이는가?

문제로 부터 얻은 것

let을 다중으로 써서 난해한 프로시저를 해석하는 능력이 조금 상승했습니다.

문제풀이

a. 동작원리

(quotient는 나눗셈의 몫을 의미합니다.)

partial-tree 프로시저의 반환값은, 인자로 받은 elts에서 왼쪽에서 n만큼의 원소를 트리로 만든뒤, 아래의 리스트를 반환하는 프로시저입니다.

'(방금만든_트리 
  elts에서_남은_원소_1 
  elts에서_남은_원소_2 
  ...)

트리를 만드는 과정에서 left-tree를 partial-tree로 만들면, partial-tree의 첫번째 원소가 left-tree이고 나머지 원소가 남은 엘리먼트들이므로, 이 엘리먼트들로 right-tree를 만들어 병합해가는 원리입니다.
즉, 이 프로시저는 반환값인 리스트의 첫번째 원소에 넣을 트리를 만들기 위해, 리스트의 나머지 부분들에서 조금씩 원소를 가져오는 메커니즘을 가진 프로시저입니다.

b. 자람차수

T(n)을 n을 인자로 가지는 partial-tree의 자람차수라고 하겠습니다. T(n)으로부터 T(2n)을 유추할 수 있습니다. T(2n)은 T(n)을 왼쪽 트리와 오른쪽 트리에 사용하므로, $T(2n)=2×T(n)$이 성립합니다.
즉 partial-tree의 자람차수는 $Θ(n)$입니다.

읽어주셔서 감사합니다.