SICP 연습문제 2.69 친절한 풀이

,
글자-빈도 쌍으로 허프만 트리 만들기

문제

다음 프로시저는 (서로 다른 두 쌍 속에 같은 글자가 들어 있지 않도록) 글자-빈도 쌍으로 이루어진 리스트를 인자로 받아서 허프만 알고리즘에 따라 인코딩 나무를 만들어 낸다.

(define (generate-huffman-tree pairs)
  (successive-merge (make-leaf-set pairs)))

make-leaf-set는 쌍 리스트를 인자로 받아서, 차례 매긴 나뭇잎 집합으로 바꿔주는 프로시저인데, 이것은 본문에서 정의한 것과 같다. make-code-tree 프로시저를 써서, 집합에 원소 하나만 남을 때까지, 곧 허프만 나무를 만들 때까지 가장 가벼운 두 원소를 잇달아 묶어내는 successive-merge 프로시저를 짜라. (이 프로시저를 짜려면 조금 잔재주를 부려야 하지만, 복잡한 것은 아니다. 따라서 복잡한 프로시저를 설계한다면, 뭔가 잘못하고 있다고 보면 틀림없다. 이때, 차례매긴 집합 표현 방식을 쓴다는 사실에서 큰 도움을 얻을 수 있다.)

문제로 부터 얻은 것

개인적으로 시간이 굉장히 많이 걸린 문제였습니다.
이 문제를 잘 풀기 위해서는 몇가지를 잘 파악했어야 했습니다.
첫째로 이파리들을 트리로 엮어내기 전에 adjoint를 사용해야 했습니다.
둘째로 make-leaf-set은 '오름차순으로 정렬’된 이파리 리스트를 반환하는데, 이 점을 유념했어야 했습니다.
셋째로 pairs가 글자-빈도 쌍인지 모르고, 글자만으로 프로시저를 짜려고 했다가 시간을 낭비해버렸습니다.

문제풀이

a. 기본 프로시저

문제 풀이에 필요한 기본 프로시저들입니다.

(define (make-leaf symbol weight)
  (list 'leaf symbol weight))
(define (leaf? object)
  (eq? (car object) 'leaf))
(define (symbol-leaf object)
  (cadr object))
(define (weight-leaf object)
  (caddr object))

(define (symbols tree)
  (if (leaf? tree)
    (list (symbol-leaf tree))
    (caddr tree)))

(define (weight tree)
  (if (leaf? tree)
    (weight-leaf tree)
    (cadddr tree)))

(define (make-code-tree left right)
  (list left
        right
        (append (symbols left) (symbols right))
        (+ (weight left) (weight right))))

(define (adjoin-set x set)
  (cond ((null? set) (list x))
        ((< (weight x) (weight (car set))) (cons x set))
        (else (cons (car set)
                    (adjoin-set x (cdr set))))))



b. make-leaf-set

make-leaf-set은 문자-빈도 쌍을 정렬하는 프로시저입니다. 트리를 weight에 따라 정렬하기 위해 책에서 제시한 adjoin-set 프로시저를 이용하면 쉽게 구현할 수 있습니다. 문자-빈도 쌍을 leaf로 만들어서 집합에 넣어주면 됩니다.

(define (make-leaf-set pairs)
  (if (null? pairs)
      '()
      (adjoin-set (make-leaf (caar pairs)
                             (cadar pairs))
                  (make-leaf-set (cdr pairs))))



c. successive-merge

정말 시간이 오래 걸린 프로시저였습니다.

가장 처음 떠올린 아이디어는 pairs의 가장 처음 원소 세가지를 비교해가면서, 합이 가장 작은 쌍을 골라서 tree로 만들어가는 프로시저였습니다. 하지만, pairs는 오름차순으로 정렬된 리스트입니다. 가장 작은 쌍은 항상 맨 앞의 두개입니다.

또, 맨 앞의 두개를 트리로 만든다고 해도 다른 리스트들 사이에 크기 순으로 정렬을 해야 합니다. 그런데, 문제를 풀 당시에는 adjoin-set의 존재를 잊어버리고 있었습니다. 무엇인가 트리를 정렬한다는 느낌이 나오면, 항상 adjoin-set을 떠올리는 습관을 들여야겠습니다.

만든 프로시저는 다음과 같습니다.

(define (generate-huffman-tree pairs)
  (successive-merge (make-leaf-set pairs)))

(define (successive-merge tree)
  (define (successive-merge-iter tree)
  (cond ((null? (cdr tree))
         tree)
        ((null? (cddr tree))
         (make-code-tree (car tree) (cadr tree)))
        (else
         (successive-merge-iter
          (adjoin-set
           (make-code-tree (car tree) (cadr tree))
           (cddr tree))))))
  (successive-merge-iter tree))



아래의 코드를 실행해서 프로시저를 테스트해 보겠습니다.

(generate-huffman-tree '((A 1) (F 6) (C 3) (B 2) (D 4) (E 5)))

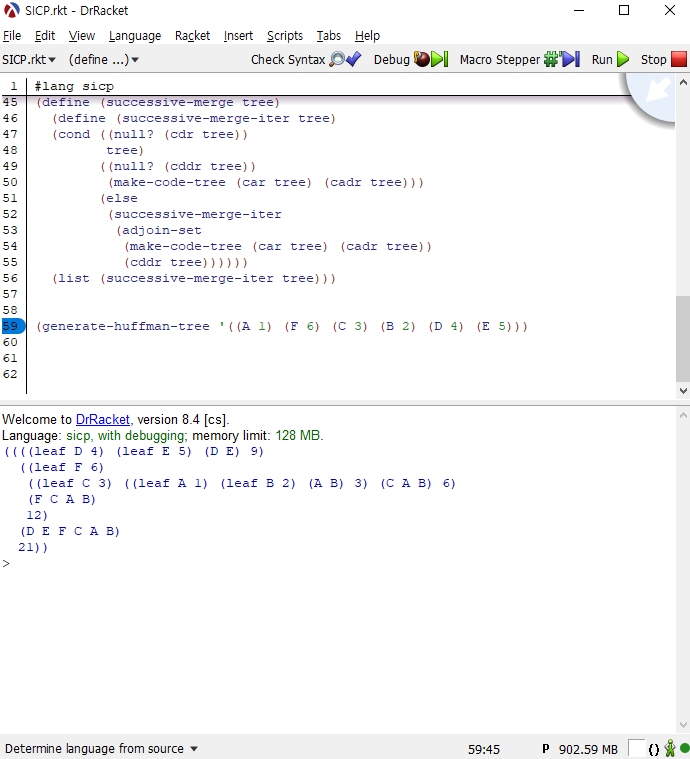
프로시저가 만들어낸 허프만 코드



위의 코드를 도식화하겠습니다.
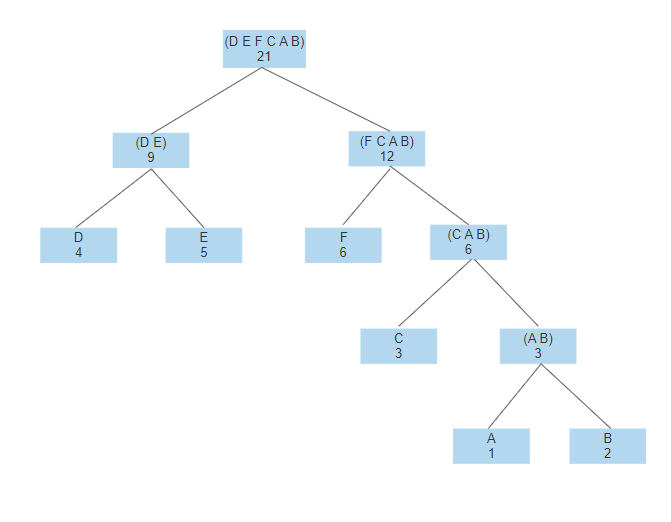
발로 그린듯한 트리



이딴게 허프만 트리? 라고도 할 수 있겠지만, 우선순위에 따라 높이가 다른 엄연한 허프만 트리입니다.

읽어주셔서 감사합니다.