SICP 연습문제 2.7 친절한 풀이

문제

Alyssa가 짠 프로그램에는, 구간 값을 나타내는 요약된 데이터가 있다고 보고 구간 산술 연산을 만들었다. 그러므로 Alyssa의 프로그램을 돌아가게 만들려면, 실제로 구간 데이터를 만들어야 한다. 구간을 짜맞추는 연산이 아래와 같다고 하자.

(define (make-interval a b) (cons a b))

이를 바탕으로, 구간의 상한과 하한을 골라내는 upper-bound와 lower-bound를 정의하여 Alyssa의 프로그램을 돌아가게 만들어라.

문제로 부터 얻은 것

구간 산술 연산에 대한 지식을 얻을 수 있습니다.
또 그 연산을 프로시저로 구현하는 법을 배울 수 있습니다.

문제풀이

문제 자체를 푸는 것은 어렵지 않습니다.
답은 당연히 아래와 같습니다.

(define (make-interval a b) (cons a b))

(define (upper-bound x) (cdr x))
(define (lower-bound x) (car x))

이 문제의 가치는 2.1.4절의 구간 산술 연산을 이해하는 데에 있습니다.
책에 적힌 기본 산술 연산들은 아래와 같습니다.

(define (add-interval x y)
  (make-interval (+ (lower-bound x) (lower-bound y))
                 (+ (upper-bound x) (upper-bound y))))
         
(define (mul-interval x y)
  (let ((p1 (* (lower-bound x) (lower-bound y)))
        (p2 (* (lower-bound x) (upper-bound y)))
        (p3 (* (upper-bound x) (lower-bound y)))
        (p4 (* (upper-bound x) (upper-bound y))))
    (make-interval (min p1 p2 p3 p4)
                   (max p1 p2 p3 p4))))

(define (div-interval x y)
  (mul-interval x
                (make-interval (/ 1.0 (upper-bound y))
                               (/ 1.0 (lower-bound y)))))

위의 프로시저들을 이용해서 책의 2.1.4절에 나온 저항 합성 문제를 계산해 보도록 하겠습니다.

$R_p = \frac{1}{1/R_1 + 1/R_2}$

R1을 6.8Ω에 허용오차 10%
R2를 4.7Ω에 허용호차 5%라고 한다면,

각각의 범위는 아래와 같습니다.
R1 = 6.12 ~ 7.48
R2 = 4.46 ~ 4.93

위에서 구현한 프로시저들이 정확하다면 R1과 R2의 합성 Rp는 2.58~2.97이어야 합니다.
Rp를 구하는 프로시저는 다음과 같습니다.
아래의 프로시저에서 one은 범위가 1부터 1까지인 구간입니다.

(define (Rp R1 R2)
  (let ((one (make-interval 1.0 1.0)))
    (div-interval one
                  (add-interval (div-interval one R1)
                                (div-interval one R2)))))

그리고 아래의 코드를 실행시켰습니다.

(define R1 (make-interval 6.12 7.48))
(define R2 (make-interval 4.46 4.93))

(Rp R1 R2)

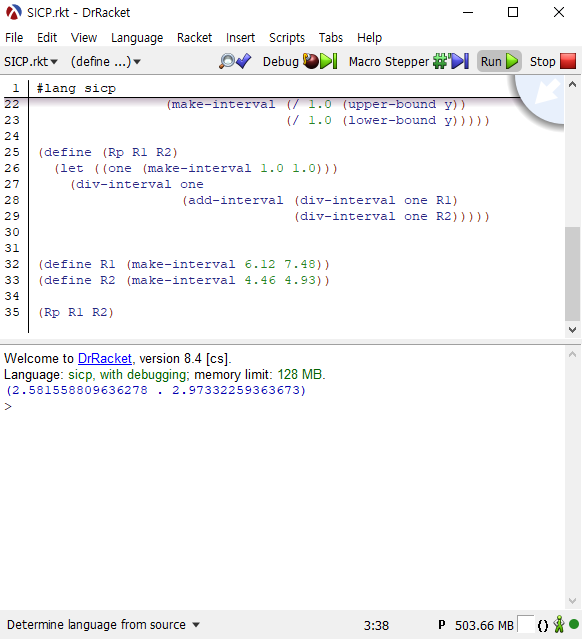
예상한 범위의 값을 산출하는 모습입니다.

읽어주셔서 감사합니다.