SICP 연습문제 2.71 친절한 풀이

문제

글자 N개를 위한 허프만 트리가 있고, 글자마다 빈도가 $1,2,3,4, ⋯ , 2^{n-1}$이라고 하자. $n=5$일 때와 $n=10$일 때 나무를 스케치해 보라. 그런 나무에서 (글자 수가 n이라고 할 때) 가장 많이 나오는 글자와 가장 덜 나오는 글자를 인코딩 하는 데 얼마나 많은 비트가 필요한가?

문제로 부터 얻은 것

허프만 트리의 가장 빈도수가 낮은 글자의 인코딩 비트 자리수는 n에 비례한다는 것을 알았습니다.

문제풀이

a. 트리 스케치

각각 $n=5$일 때와 $n=10$일 때 나무를 스케치한 모습입니다.

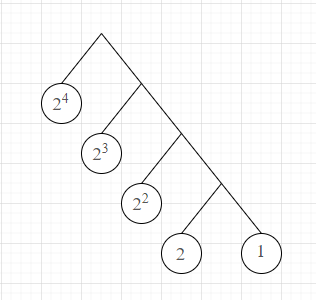
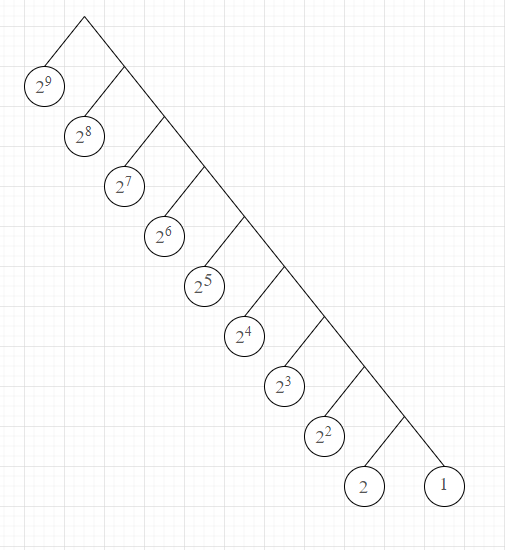
b. 빈도수에 따라 필요한 비트수

$n=5$인 허프만 트리에서 빈도가 가장 높은 $2^4$의 빈도를 가지는 글자는, 뿌리에서 부터 왼쪽으로 1만큼 떨어져 있으므로 인코딩할때 '0’으로 표현됩니다. 빈도수가 가장 낮은 $1$의 빈도를 가지는 글자는 뿌리로부터 오른쪽으로 4만큼 떨어져 있으므로, "1111"로 표현됩니다. 즉, 가장 높은 빈도수의 글자는 1자리의 비트가 필요하고, 가장 낮은 빈도수의 글자는 4자리의 비트가 필요합니다.

$n=10$인 허프만 트리에서 빈도가 가장 높은 $2^9$의 빈도를 가지는 글자는, 뿌리에서 부터 왼쪽으로 1만큼 떨어져 있으므로 인코딩할때 '0’으로 표현됩니다. 빈도수가 가장 낮은 $1$의 빈도를 가지는 글자는 뿌리로부터 오른쪽으로 9만큼 떨어져 있으므로, "111111111"로 표현됩니다. 즉, 가장 높은 빈도수의 글자는 1자리의 비트가 필요하고, 가장 낮은 빈도수의 글자는 9자리의 비트가 필요합니다.

결국 모든 허프만 트리에서 가장 높은 빈도수의 글자는 $1$비트가 필요하고, 가장 낮은 빈도수의 글자는 $n-1$비트가 필요합니다.

읽어주셔서 감사합니다.