SICP 연습문제 2.72 친절한 풀이

문제

연습문제 2.68에서 설계한 인코딩 프로시저를 생각해 보자. 한 글자를 인코딩하는 데 필요한 계산 단계는 어떤 자람 차수^{order of growth}를 보이는가? 마디 하나를 거쳐 갈 때마다, 글자 리스트를 훑어보는 데 들어가는 계산 단계까지 모두 아울러야 함을 잊지 마라. 이 문제의 일반해^{general solution}을 구하기는 어렵다. 글자 n개의 빈도가 연습문제 2.71과 같은 경우만 따져서, 가장 많이 쓰는 글자와 가장 적게 쓰는 글자를 인코딩하는 데 얼마나 많은 계산 단계를 밟아야 하는지 (n의 함수로 정의한) 자람차수로 나타내라.

문제로 부터 얻은 것

허프만 트리로 문자를 인코딩할때, 빈도수가 낮아질 수록 시간복잡도가 많이 증가한다는 것을 알 수 있었습니다.

문제풀이

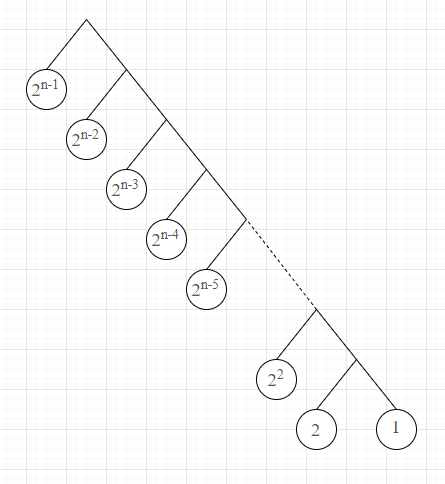
가장 높은 빈도의 글자를 찾는 계산단계는 쉽게 떠올릴 수 있습니다. 뿌리의 문자열 중에서 가장 왼쪽에 있는 글자이기 때문에, 1만큼의 검색시간만 필요할 뿐입니다.

빈도수가 낮아질수록 검색시간은 당연하게도 늘어납니다. 2번째로 높은 빈도수의 글자를 찾기 위해서는 두단계의 과정을 거쳐야 합니다. 첫번째 단계는 뿌리의 왼쪽에 있는 노드인지, 오른쪽에 있는 노드인지 확인하는 작업입니다. 이 작업은 단순하게 문자열을 왼쪽에서부터 차례대로 탐색하는 것으로 생각할 수 있습니다. 지금 찾으려는 문자는 전체 문자열의 왼쪽에서 2번째에 있으므로 2만큼의 검색시간이 필요합니다. 이 작업이 끝나면 두번째로 높은 빈도수의 문자가 문자열의 가장 첫번째에 있는 트리에서 또다시 검색을 해야 합니다. 이때 찾는 문자는 문자열의 첫번째에 있으므로 1만큼의 검색시간이 필요합니다. 총 검색시간은 3입니다.

위의 과정에서 유추할 수 있는 사실이 있습니다. n번째로 빈도수가 높은 문자를 찾기 위해서는 $n + (n-1) + (n-2) + ⋯ + 1$만큼의 검색시간이 필요하다는 것입니다. 이 검색시간은 $1$부터 $n$까지의 등차수열의 합이므로, $\frac{(1+n)n}{2}$입니다.

즉, 가장 높은 빈도수를 찾는 경우의 시간복잡도는 $Θ(1)$이고 가장 낮은 빈도수를 찾는 경우의 시간 복잡도는 $Θ(n^2)$입니다.

읽어주셔서 감사합니다.