SICP 연습문제 1.19 친절한 풀이

문제

피보나치 수열을 구하는 계산 단계가 로그 차수로 자라나도록 만든 똑똑한 알고리즘이 있다. 1.2.2절에서 나온 fib-iter 프로세스에서 상태변수 a와 b를 바꾸는 규칙 $a ← a+b$, $b ← a$가 생각나는가? 이 규칙을 T라고 할 때, 1과 0을 첫 값으로 놓고 T를 n번 하고 나면 Fib(n+1)와 Fib(n)을 얻을 수 있다. 다시말해 $T^n$ 곧 (1,0)에서 T를 n번 거듭 곱하면 피보나치 수열이 나온다. T_pq가 (a,b)를 두고 $a ← bq+aq+ap$와 $b ← bp+aq$라는 규칙을 가리킨다고 하면, 이제는 T가 T_pq에서 p=0,q=1인 경우를 나타낸다고 볼 수 있다. T_pq를 두번 거듭 계산할 때 나온 값이, T_$p'q'$을 한 번 한 것과 같다는 것을 밝히고, p와 q로 $p^{\prime}$과 $q^{\prime}$를 계산하는 식도 밝혀 보아라.

문제로 부터 얻은 것

수학적인 내용을 이해하면
프로그램의 로직을 개선시킬 수 있다는 것을 알았습니다.

문제풀이

수식이 난해할 수 있으니 천천히 읽어주시기 바랍니다.

a, b의 초기값을 a₁,b₁이라고 합시다.

그렇다면 a₁,b₁에 T연산을 적용시킨 결과물인 a₂,b₂은 아래와 같습니다.
a₂=b₁q+a₁q+a₁p
b₂=b₁p+a₁q

마찬가지로 a₃,b₃는 아래와 같습니다.

a₃
= b₂q+a₂q+a₂p
= (b₁p + a₁q)q + (b₁q + a₁q + a₁p)q + (b₁q + a₁q + a₁p)p

b₃
= b₂p+a₂q
= (b₁p + a₁q)p + (b₁q + a₁q + a₁p)q

식을 잘 풀어서 정리하면,
작성자의 편의를 위해 a₁,b₁은 a,b로 표시하겠습니다.
a₃ $= b(q^2+2pq)+a(p^2+q^2+q^2+2pq)$
b₃ $= b(p^2+q^2)+a(2pq+q^2)$

$p^{\prime}=p^2+q^2$
$q^{\prime}=q^2+2pq$
라고 한다면,

a₃ $=bq^{\prime}+aq^{\prime}+ap^{\prime}$
b₃ $=bp^{\prime}+aq^{\prime}$
이 성립합니다.

즉 p와 q의 값만 $p^{\prime}$,$q^{\prime}$으로 바꿔주면, T연산을 두번한 효과를 볼 수 있습니다.

따라서 구하고자 하는 프로시저는 아래와 같습니다.

(define (fib-iter a b p q count)
  (cond ((= count 0) b)
        ((even? count)
         (fib-iter a
                   b
                   (+ (square p) (square q)) 
                   (+ (square q) (* 2 p q))
                   (/ count 2)))
        (else (fib-iter (+ (* b q) (* a q) (* a p))
                        (+ (* b p) (* a q))
                        p
                        q
                        (- count 1)))))

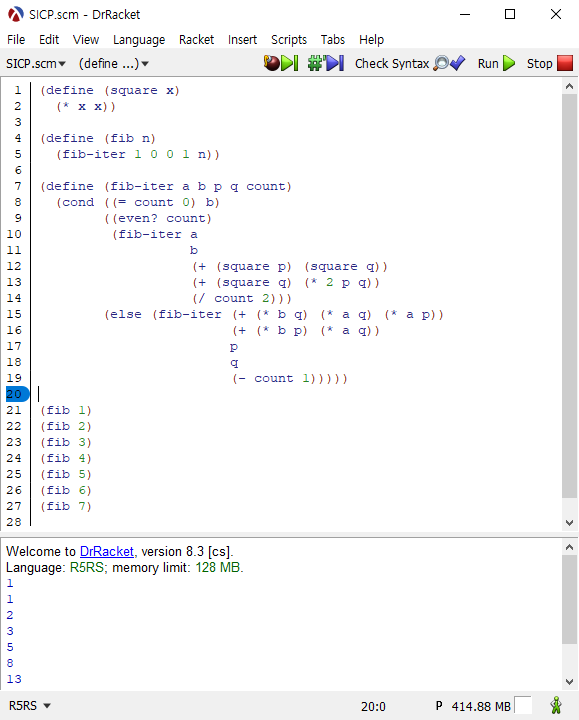
이번 문제는 수학적인 내용을 이해하면 프로그램을 짤 때, 더 효율적으로 짤 수 있다는 것을 보여준 예시입니다.
글로는 이해가 잘 안되실 겁니다. 직접 노트에 수식을 계산해 보면서 수학에 아름다움을 느끼셨으면 좋겠습니다.
프로그래밍을 깊이있게 배운다는 것은 무엇을 할지보다 어떻게 할지에 중점을 둔 것이기 때문에 이런 문제들도 풀어보는 것 같습니다.
count가 짝수일 때와 홀수일 때를 나누는 아이디어는 연습문제 1.16, 연습문제 1.17 에서 충분히 다루었기 때문에 언급하지는 않겠습니다.

읽어주셔서 감사합니다.