SICP 연습문제 1.23 친절한 풀이

문제

이 절 처음에 만든 smallest-divisor 프로시저는 쓸모없는 검사를 너무 많이 한다. 다시 말해서, 어떤 수가 2로 나뉜다면 다시 그 수가 더 큰 짝수로 나뉘는 지 알아볼 까닭이 없기 때문이다. 이 말은 test-divisor에서 2,3,4,5,6…이 아니라 2,3,5,7,9…를 써야 한다는 뜻이다. 이 생각에 따라 2가 들어오면 3을 그 밖의 값이 들어오면 2를 더한 값을 내놓은 프로시저 next를 만들어라. 그리고 (+ test-divisor 1)대신 (next test-divisor)를 쓰도록 smallest-divisor프로시저를 고쳐라. 그런 다음 timed-prime-test로 연습문제1.22에서 찾은 소수 12개를 다시 검사해 보라. 검사 횟수가 반으로 줄었으니 계산도 두배로 빨라지는가? 그렇지 않다면 두 알고리즘의 빠르기를 견줄 때 그 진짜 비율은 어림잡아 얼마인가?

문제로 부터 얻은 것

이론과 실제는 많이 다르다.

문제풀이

문제의 조건에 맞게 next프로시저를 만들고 기존의 프로시저와의 비교를 위해 새로운 new-프로시저들을 만들었습니다.

(define (next n)
  (if (= n 2)
      3
      (+ n 2)))

(define (new-find-divisor n test-divisor)
  (cond ((> (square test-divisor) n) n)
        ((divides? n test-divisor) test-divisor)
        (else (find-divisor n (next test-divisor)))))

(define (new-smallest-divisor n)
  (new-find-divisor n 2))

(define (new-prime? n)
  (= (new-smallest-divisor n) n))

(define (new-timed-prime-test n)
  (new-start-prime-test n (runtime)))

(define (new-start-prime-test n start-time)
  (if (new-prime? n)
      (report-prime (- (runtime) start-time) n)))

그리곤 테스트케이스를 몇개 실행시켜 보았습니다.

(display "orginal")
(timed-prime-test 10000000033)
(timed-prime-test 10000000033)
(timed-prime-test 10000000033)
(newline)
(display "new")
(new-timed-prime-test 10000000033)
(new-timed-prime-test 10000000033)
(new-timed-prime-test 10000000033)

결과는 예상 밖이었습니다.

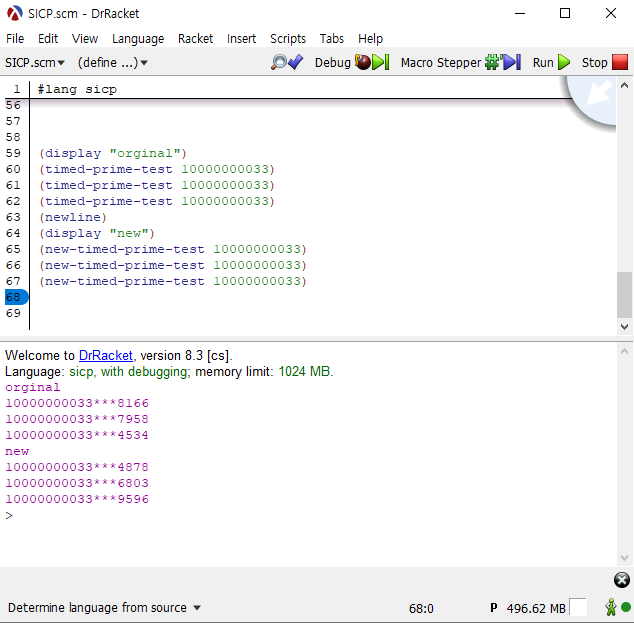
별로 큰 차이가 없었습니다.
다른 사이트의 결과물들을 보면 "1.6배정도 빨랐다. " "1.5배정도 빨랐다. "같은 말들이 많은데 저는 몇번을 돌려 보았지만 큰 차이를 보지 못했습니다.
원래 이 문제의 정답은 "if문을 실행하는 데에도 시간이 걸리기 때문에 정확히 2배는 아니다. "입니다.
그런데 제 실행 결과는 1.5배는 커녕 1배정도 되는 것 같습니다.
if의 실행시간이 생각보다 오래걸리나 봅니다.

if없이 구현

이번에는 실험의 일환으로 next프로시저 대신 처음부터 (+ new-divisor 2)를 써서
if문을 없애 보도록 하겠습니다.
이렇게 하면 실행시간이 반으로 줄지 않을까 싶었습니다.

(define (new-find-divisor n test-divisor)
  (cond ((> (square test-divisor) n) n)
        ((divides? n test-divisor) test-divisor)
        (else (find-divisor n (+ test-divisor 2)))))

(define (new-smallest-divisor n)
  (new-find-divisor n 3))

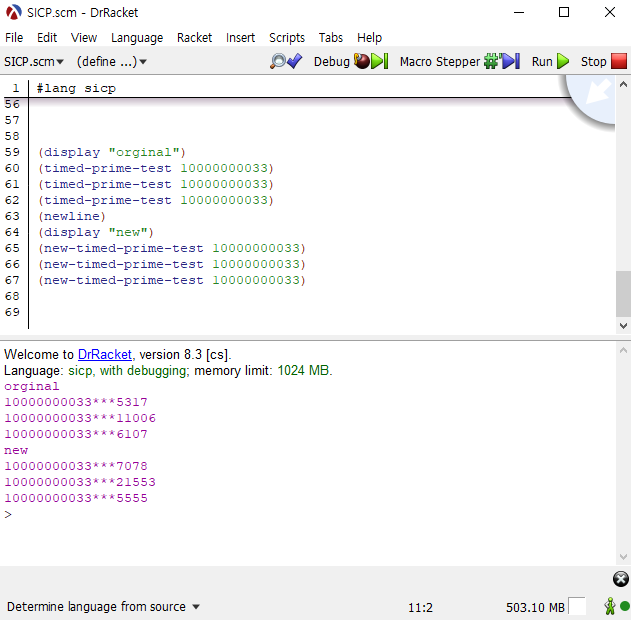
ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ

이전 보다는 확실히 빨리 계산되는 경우가 많았습니다.
그럼에도 별로 나아진 것이 없어보입니다.
이론과 실제가 많이 다르다는 것을 느낄 수 있는 하루였습니다.

허접한 글 읽어주셔서 감사합니다.