SICP 연습문제 1.24 친절한 풀이

문제

연습문제 1.22의 timed-prime-test를 fast-prime?(페르마 검사)를 쓰도록 고친 다음에, 연습문제에서 찾아낸 소수 12개를 다시 검사해 보자. 페르마 검사는 $Θ(\log{n})$정도로 자라나므로 1,000,000 언저리 소수를 찾을 때와 1,000 언저리 소수를 찾을 때 걸리는 시간이 얼마나 차이난다고 볼 수 있는가? 그 생각이 실험 결과와 맞아 떨어지는가? 잘 맞아 떨어지지 않는다면, 그 까닭을 설명할 수 있겠는가?

문제로 부터 얻은 것

이론과 실제는 다르다.

문제풀이

새로운 prime?과 그외 프로시저들은 다음과 같이 구상했습니다.

(define (square x)
  (* x x))

(define (report-prime elapsed-time)
  (display "***")
  (display elapsed-time))

(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (remainder (square (expmod base (/ exp 2) m))
                    m))
        (else
         (remainder (* base (expmod base (- exp 1) m))
                    m))))

(define (fermat-test n)
  (define (try-it a)
    (= (expmod a n n) a))
  (try-it (+ 1 (random (- n 1)))))

(define (prime? n times)
  (cond ((= times 0) true)
        ((fermat-test n) (prime? n (- times 1)))
        (else false)))

(define (start-prime-test n start-time)
  (if (prime? n 100)
      (report-prime (- (runtime) start-time) n)))

(define (timed-prime-test n)
  (start-prime-test n (runtime)))

위의 코드를 보시면 아시겠지만, 페르마 검사를 하는 횟수는 100으로 설정하였습니다.
다음의 소수 12개에 대해 시간을 재보겠습니다.

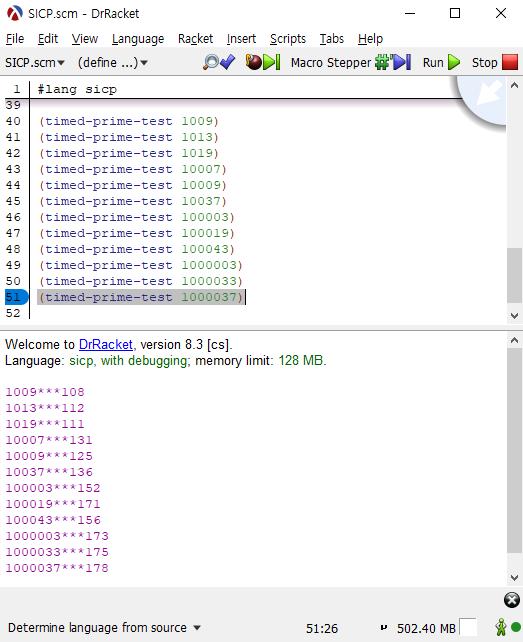
(timed-prime-test 1009)
(timed-prime-test 1013)
(timed-prime-test 1019)
(timed-prime-test 10007)
(timed-prime-test 10009)
(timed-prime-test 10037)
(timed-prime-test 100003)
(timed-prime-test 100019)
(timed-prime-test 100043)
(timed-prime-test 1000003)
(timed-prime-test 1000033)
(timed-prime-test 1000037)

이론상 페르마 검사는 $Θ(\log{n})$정도로 자라나므로
1,000 언저리의 수와 1,000,000 언저리의 수는 두배의 속도차이가 나야 합니다.

얼추 두배인것 같기도 하지만 역시나 약간의 차이가 있습니다.
if식을 포함한 다른 프로시저들은 $Θ(\log{n})$에 표시되어 있지 않기 때문에 생기는 현상입니다.

또다시 이전의 문제들과 같은 결론을 내려야할 것 같습니다.
이론과 실제는 다르다.

참고로 위 expmod프로시저가 이해가 되지 않으신다면 이 글을 추천합니다.

읽어주셔서 감사합니다.