SICP 연습문제 1.26 친절한 풀이

문제

Louis Reasoner는 연습문제 1.24를 푸느라 애를 많이 썼다. 그런데 fast-prime?이 prime 보다 훨씬 느린 듯 보였다. Louis는 친구인 Eva Lu Ator보고 도와 달라고 하였다. 그래서 Eva Louis의 프로그램을 살펴보았더니, expmod가 square를 부르지 않고 그냥 곱셈을 쓰고 있었다.

(define (expmod base exp m)
  (cond((= exp 0) 1)
       (even? exp)
         (remainder (* (expmod base (/ exp 2) m)
                       (expmod base (/ exp 2) m))
                    m)
       (else
         (remainder (* base (expmod base (- exp 1) m))
                    m))))

"이렇게 하면 뭐가 달라?"하면서 Louis가 Eva는 "난 알겠는데?"하면서 그 까닭을 이렇게 설명했다. "이거 봐. 프로시저를 이러게 쓰면 $Θ(\log{n})$프로시저가 $Θ(n)$프로시저가 되어 버린단 말이아. " Eva의 말이 무슨 뜻일까?

문제로 부터 얻은 것

square 프로시저를 곱연산으로 처리하면
한번만 실행해도 될 프로시저를 두번 실행하게 될 수도 있다는 것을 알았습니다.

문제풀이

기존의 프로시저와 달라진 것을 생각해 보겠습니다.

(square (expmod base (/ exp 2) m))

(* (expmod base (/ exp 2) m)
   (expmod base (/ exp 2) m))

위의 식에서는 제곱을 하기 위해 expmod를 한번만 계산하면 됩니다.
반면, 아래의 식에서는 곱셈연산을 하기 위해 expmod를 두번 계산해야 합니다.

즉, 기존에 비해 expmod를 두 배 사용하는 것입니다.

처음에는 n이 2n이 되어서 $Θ(\log{2n})$이 되므로 성능에 큰 차이는 없는 것이 아닌가? 하는 의문이 들었습니다.
하지만 조금 생각해 보니 왜 $Θ(n)$이 되는지 알 수 있었습니다.

square를 단순곱셈으로 고치게 되면, 단지 그 연산에서만 영향을 주는 것이 아닙니다.
그 프로시저의 다음 프로시저까지 영향을 주게 되는 것입니다.

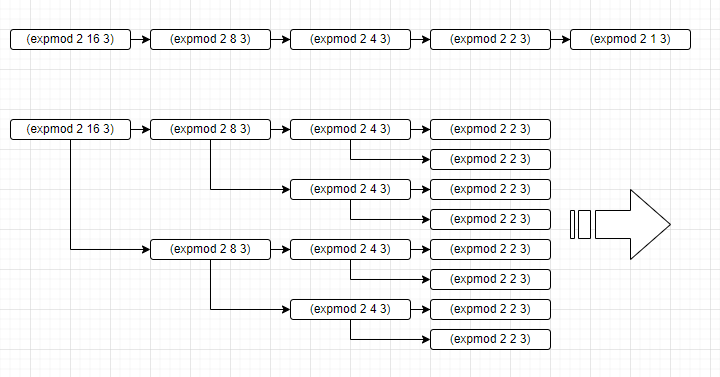
위의 다이어그램을 보시면, 기존의 프로시저에 비해 $2^n$만큼의 수행을 더 하는 것을 볼 수 있습니다.

즉 프로시저의 시간복잡도는
$Θ(\log{n})$ 에 $(n≤ftarrow 2^n)$을 대입한,
$Θ(n)$이 되는 것입니다.

읽어주셔서 감사합니다.