SICP 연습문제 2.15 친절한 풀이

문제

Alyssa의 시스템을 써본 또 다른 사용자 Eva Lu Ator는 대수적으로 같은 식이지만 다른 식이 있을 때 계산된 구간 값이 다르게 나오는 문제점을 또 알아차렸다. Alyssa의 시스템으로 구간 계산을 할 때 부정확한 수를 나타내는 변수가 있는데, 그 변수를 되풀이해서 쓰지 않는 어떤 공식을 쓸 수 있으면, 그 공식이 오차 범위를 더 줄인다고 했다. 그렇게 보면, 병렬 저항을 구할 대 같은 병렬 저항을 구하는 공식이라 하더라도 par2가 par1보다 나은 프로그램이라고 말했다. 이 말이 옳은가? 그렇다면 그 까닭은 무엇인가?

문제로 부터 얻은 것

왜 구간 산술 연산에서는 대수적 차원의 동치를 적용하기 힘든지 알게되었습니다.
시험을 위해 테스트 케이스를 만드는 스킬의 경험치가 조금 증가했습니다.

문제풀이

연습문제 2.14에서도 보았듯, 대수적 차원에서 같은 표현식도 Alyssa의 시스템에서는 다른 값을 산출한다는 것을 확인했습니다.

$A/A \neq 1$

이 사례는 한 표현식에서 같은 문자가 여러번 사용될 수록 오차의 범위가 늘어난다는 것으로 일반화할 수 있습니다. 그러므로 par1보다는 par2가 더 정확한 계산법이라는 것을 알 수 있습니다.

$par1 = \frac{R_1R_2}{R_1+R_2}$

$par2 = \frac{1}{1/R_1+1/R_2}$

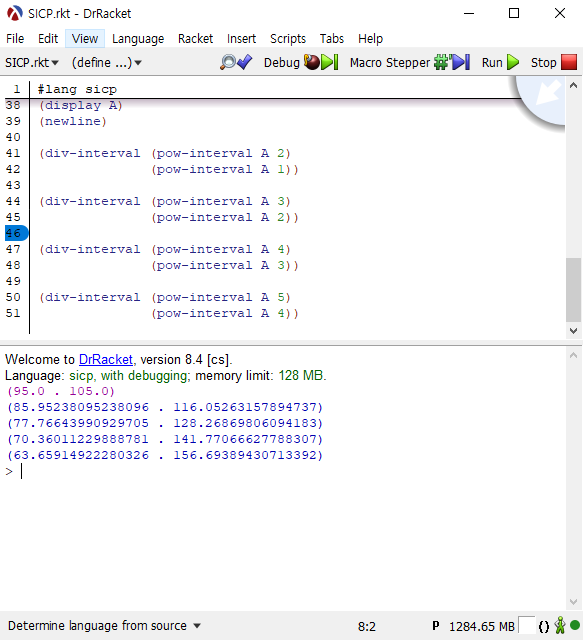
같은 문자가 여러번 사용될 수록 오차의 범위가 늘어난다는 것을 시험하기 위해 다음의 테스트코드를 실행시켜 보기로 했습니다.

$A= \frac{A^2}{A}= \frac{A^3}{A^2} = \frac{A^4}{A^3}= ⋯$

계산을 도와줄 pow-interval 프로시저입니다. $b^n$을 구하는 프로시저입니다.

(define (pow-interval b n)
  (if (= n 0)
      (make-interval 1.0 1.0)
      (mul-interval b
                    (pow-interval b (- n 1)))))

A는 $(95, 105)$입니다.

(define A (make-center-percent 100 5))

(display A)
(newline)

(div-interval (pow-interval A 2)
              (pow-interval A 1))

(div-interval (pow-interval A 3)
              (pow-interval A 2))

(div-interval (pow-interval A 4)
              (pow-interval A 3))

(div-interval (pow-interval A 5)
              (pow-interval A 4))

산출되는 값에서 A가 많아질 수록, 오차가 커지는 것을 확인할 수 있습니다.

읽어주셔서 감사합니다.