SICP 연습문제 2.65 친절한 풀이

문제

연습문제 2.63과 연습문제 2.64에서 얻은 결과를 빌려서, (균형잡힌) 두 갈래 나무로 집합을 표현하였을 때, 집합연산 union-set과 intersection-set의 자람차수가 $Θ(n)$이 되도록 구현하라.

문제로 부터 얻은 것

프로시저를 구성하는 개별 프로시저의 시간 복잡도를 낮추는 방법으로 전체 프로시저의 시간 복잡도를 많이 낮출 수 있다는 것을 알았습니다.

문제풀이

연습문제 2.63과 연습문제 2.64 그리고 연습문제 2.62에서 얻은 결과물입니다.

(define (tree->list tree)
  (define (copy-to-list tree result-list)
    (if (null? tree)
        result-list
        (copy-to-list (left-branch tree)
                      (cons (entry tree)
                            (copy-to-list (right-branch tree)
                                          result-list)))))
  (copy-to-list tree '())) 
  
(define (list->tree elements)
  (car (partial-tree elements (length elements))))

(define (partial-tree elts n)
  (if (= n 0)
      (cons '() elts)
      (let ((left-size (quotient (- n 1) 2)))
        (let ((left-result (partial-tree elts left-size)))
          (let ((left-tree (car left-result))
                (non-left-elts (cdr left-result))
                (right-size (- n (+ left-size 1))))
            (let ((this-entry (car non-left-elts))
                  (right-result (partial-tree (cdr non-left-elts)
                                              right-size)))
              (let ((right-tree (car right-result))
                    (remaining-elts (cdr right-result)))
                (cons (make-tree this-entry left-tree right-tree)
                      remaining-elts))))))))

(define (union-set set1 set2)
  (cond ((null? set1) set2)
        ((null? set2) set1)
        (else
         (let ((x1 (car set1))
               (x2 (car set2)))
           (cond ((null? set1) set2)
                 ((null? set2) set1)
                 ((= x1 x2) (cons x1
                            (union-set (cdr set1) (cdr set2))))
                 ((> x1 x2) (cons x2
                            (union-set set1 (cdr set2))))
                 ((< x1 x2) (cons x1
                            (union-set set2 (cdr set1)))))))))

a. union-set

제가 떠올린 아이디어는 이렇습니다. 트리를 집합연산을 하기 편하게 list로 바꾼뒤, 합집합 연산을 합니다. 또 이 합집합을 다시 트리로 바꾸면 문제는 해결됩니다. 트리를 list로 바꾸는 프로시저는 $Θ(n)$으로 해결할 수 있습니다. 리스트가 정렬된 리스트이므로 합집합 연산도 $Θ(n)$으로 해결할 수 있습니다. 리스트를 다시 트리로 바꾸는 프로시저도 $Θ(n)$으로 해결할 수 있습니다. 즉, $Θ(n)$의 연산을 연속으로 3번 수행하므로, 전체 과정도 $Θ(n)$의 시간복잡도를 따른다고 할 수 있습니다.

(define (union-set-tree s1 s2)
  (list->tree (union-set (tree->list s1)
                         (tree->list s2))))

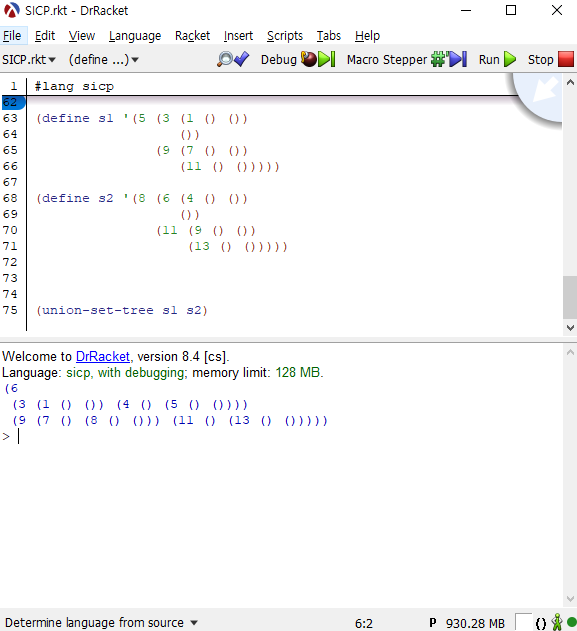
아래의 균형잡힌 트리로 프로시저를 테스트해 보겠습니다.

(define s1 '(5 (3 (1 () ())
                  ())
               (9 (7 () ())
                  (11 () ()))))

(define s2 '(8 (6 (4 () ())
                  ())
               (11 (9 () ())
                   (13 () ()))))

b. intersection-set

교집합도 합집합과 동일한 아이디어로 구현할 수 있습니다. 책의 200p에는 intersection-set이 구현되어 있습니다.

(define (intersection-set set1 set2)
  (if (or (null? set1) (null? set2))
      '()
      (let ((x1 (car set1))
            (x2 (car set2)))
        (cond ((= x1 x2)
               (cons x1
                     (intersection-set (cdr set1)
                                       (cdr set2))))
              ((< x1 x2)
               (intersection-set (cdr set1) set2))
              ((> x1 x2)
               (intersection-set set1 (cdr set2)))))))

(define (intersection-set-tree s1 s2)
  (list->tree (union-set (tree->list s1)
                         (tree->list s2))))

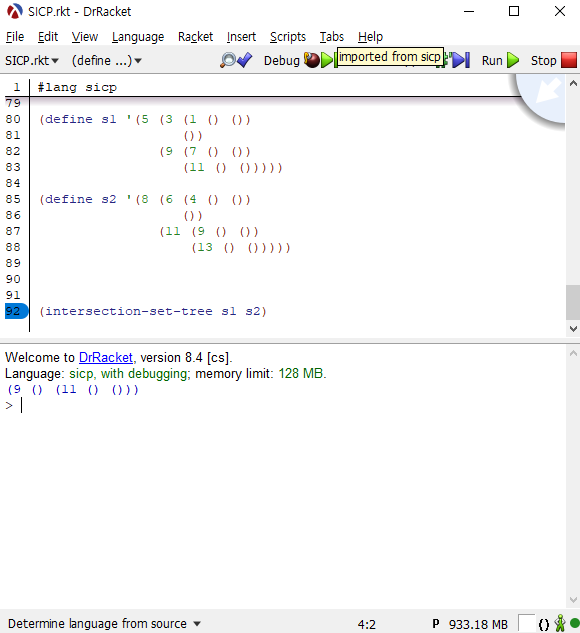
위와 동일한 테스트 코드에 차집합을 적용해 보겠습니다.

(define s1 '(5 (3 (1 () ())
                  ())
               (9 (7 () ())
                  (11 () ()))))

(define s2 '(8 (6 (4 () ())
                  ())
               (11 (9 () ())
                   (13 () ()))))

읽어주셔서 감사합니다.